
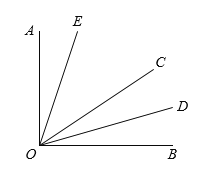
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
【答案】(1)20°;(2)36°.
【解析】试题分析:设∠AOE=x,则∠EOC=2x,∠AOC=3x,∠COB=90°-3x.根据角平分线定义得到∠COD=∠DOB=45°-1.5x.
(1)根据∠AOD=75°,列方程求解即可;
(2)由∠DOE=∠EOC+∠COD,得到45°+0.5x=54°,解方程即可得到结论.
试题解析:解:设∠AOE=x,则∠EOC=2x,∠AOC=3x,∠COB=90°-3x.∵OD平分∠COB,∴∠COD=∠DOB=![]() ∠COB=45°-1.5x.
∠COB=45°-1.5x.
(1)若∠AOD=75°,即∠AOC+∠COD=75°,则3x+45°-1.5x=75°,解得:x=20°,即∠AOE=20°;
(2)∵∠DOE=∠EOC+∠COD=2x+45°-1.5x=45°+0.5x.若∠DOE=54°,即45°+0.5x=54°,解得:x=18°,则2x=36°,即∠EOC=36°.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】棱长为a的小正方体,按照如图所示的方法一直维续摆放,自上而下分别叫第1层、第2层、……第n(n>0)层,第n层的小方体的个数记为S.
![]()


(1)完成下表:
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | _____ | _____ | … |
(2)上述活动中,自变量和因变量分别是什么?
(3)研究上表可以发现S随n的增大而增大,且有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年6月27日,四川共青图雨城区委在中里镇文化馆举办了第二期青年剪纸培训,参加培训的小王想把一块Rt△ABC废纸片剪去一块矩形BDEF纸片,如图所示,若∠C=30°,AB=10cm,则该矩形BDEF的面积最大为( )
A.4![]() cm3
cm3
B.5![]() cm3
cm3
C.10![]() cm3
cm3
D.25![]() cm3
cm3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了开展阳光体育运动,让学生每天能锻炼一小时,某学校去体育用品商店购买篮球与足球,篮球每只定价100元,足球每只定价50元.体育用品商店向学校提供两种优惠方案:①买一只篮球送一只足球;②篮球和足球都按定价的80%付款.现学校要到该体育用品商店购买篮球30只,足球x只(x>30).
(1)若该学校按方案①购买,篮球需付款 元,足球需付款 元(用含x的式子表示);
若该学校按方案②购买,篮球需付款 元,足球需付款 元(用含x的式子表示);
(2)若x=40,请通过计算说明按方案①、方案②哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,连接BD,AD=6cm,BD=8cm,∠DBC=90°,现将△AEF沿BD的方向匀速平移,速度为2cm/s,同时,点G从点D出发,沿DC的方向匀速移动,速度为2cm/s.当△AEF停止移动时,点G也停止运动,连接AD,AG,EG,过点E作EH⊥CD于点H,如图2所示,设△AEF的移动时间为t(s)(0<t<4).
(1)当t=1时,求EH的长度;
(2)若EG⊥AG,求证:EG2=AEHG;
(3)设△AGD的面积为y(cm2),当t为何值时,y可取得最大值,并求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东台教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款30000元,已知“……”,设乙学校教师有x人,则可得方程![]() ,根据此情景,题中用“……”表示的缺失的条件应补( )
,根据此情景,题中用“……”表示的缺失的条件应补( )
A. 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
B. 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
C. 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
D. 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
查看答案和解析>>
科目:初中数学 来源: 题型:
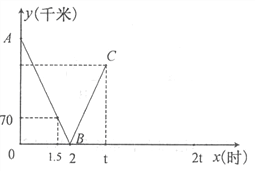
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息:
(1)求线段AB所在直线的函数解析式;
(2) 可求得甲乙两地之间的距离为 千米;
(3)已知两车相遇时快车走了180千米,则快车从甲地到达乙地所需时间为 小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
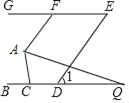
【题目】如图,已知BC∥GE,AF∥DE,∠1=56°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=14°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com