
【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.

【答案】(1)证明见解析;(2)当∠CAE=120°时,△ABC是等边三角形,证明见解析.
【解析】试题分析:
(1)由已知条件易得∠EAD=∠CAD,∠EAD=∠B,∠CAD=∠C,从而可得∠B=∠C,进一步可得AB=AC,由此即可得到△ABC是等腰三角形;
(2)由(1)可知△ABC是等腰三角形,因此当∠BAC=60°,即∠CAE=120°时,△ABC是等边三角形.
试题解析:
(1)∵AD平分∠CAE,
∴∠EAD=∠CAD,
∵AD∥BC,
∴∠EAD=∠B,∠CAD=∠C,
∴∠B=∠C,
∴AB=AC.
故△ABC是等腰三角形.
(2)当∠CAE=120°时,△ABC是等边三角形,理由如下:
∵∠CAE=120°,
∴∠BAC=180°-∠CAE=180°-120°=60°,
又∵AB=AC,
∴△ABC是等边三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了开展阳光体育运动,让学生每天能锻炼一小时,某学校去体育用品商店购买篮球与足球,篮球每只定价100元,足球每只定价50元.体育用品商店向学校提供两种优惠方案:①买一只篮球送一只足球;②篮球和足球都按定价的80%付款.现学校要到该体育用品商店购买篮球30只,足球x只(x>30).
(1)若该学校按方案①购买,篮球需付款 元,足球需付款 元(用含x的式子表示);
若该学校按方案②购买,篮球需付款 元,足球需付款 元(用含x的式子表示);
(2)若x=40,请通过计算说明按方案①、方案②哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东台教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款30000元,已知“……”,设乙学校教师有x人,则可得方程![]() ,根据此情景,题中用“……”表示的缺失的条件应补( )
,根据此情景,题中用“……”表示的缺失的条件应补( )
A. 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
B. 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
C. 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
D. 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
查看答案和解析>>
科目:初中数学 来源: 题型:
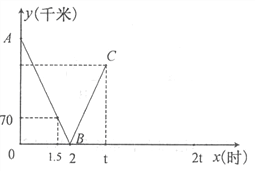
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息:
(1)求线段AB所在直线的函数解析式;
(2) 可求得甲乙两地之间的距离为 千米;
(3)已知两车相遇时快车走了180千米,则快车从甲地到达乙地所需时间为 小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.
(1)求出该品牌应急灯、手电筒的定价分别是多少元?
(2)经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
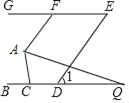
【题目】如图,已知BC∥GE,AF∥DE,∠1=56°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=14°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有( )个.
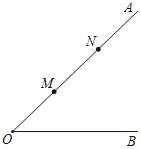
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com