
【题目】已知在平面直角坐标系中,O为坐标原点,点A的坐标为(1,a),点B的坐标为(b,1),点C的坐标为(c,0),其中a、b满足(a+b﹣8)2+|a﹣b+2|=0.
(1)求A、B两点的坐标;
(2)当△ABC的面积为6时,求点C的坐标;
(3)当4≤S△ABC≤10时,求点C的横坐标c的取值范围.
【答案】(1)A(1,3),B(5,1);(2)(1,0)或(13,0);(3)﹣3≤c≤3或11≤c≤17.
【解析】
(1)利用非负数的性质,把问题转化为方程组解决即可;
(2)分两种情形画出图形,分别构建方程即可解决问题;
(3)分两种情形分别构建不等式即可解决问题;
(1)∵(a+b﹣8)2+|a﹣b+2|=0.
∴![]() ,
,
解得![]() ,
,
∴A(1,3),B(5,1);
(2)①如图1中,当点C在直线AB的下方时,作AE⊥x轴于E,BF⊥x轴于F.设C(c,0).
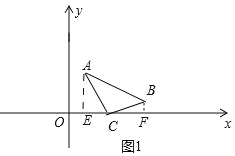
∵S△ABC=S四边形AEFB﹣S△AEC﹣S△BCF=![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×3×(c﹣1)﹣
×3×(c﹣1)﹣![]() ×1×(5﹣c)=7﹣c,
×1×(5﹣c)=7﹣c,
∴7﹣c=6
解得c=1.
②如图2中,当点C在直线AB的上方时,作AE⊥x轴于E,BF⊥x轴于F.设C(c,0).
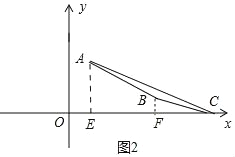
∵S△ABC=S△AEC﹣S四边形AEFB﹣S△BCF=![]() ×3×(c﹣1)﹣
×3×(c﹣1)﹣![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×1×(c﹣5)=c﹣7,
×1×(c﹣5)=c﹣7,
∴c﹣7=6,
解得c=13,
∴满足条件的点C坐标为(1,0)或(13,0).
(3)由(2)可知,当点C在直线AB下方时,S△ABC=7﹣c,
∴4≤7﹣c≤10,
∴﹣3≤c≤3,
当点C在直线AB是上方时,S△ABC=c﹣7,
∴4≤c﹣7≤10,
∴11≤c≤17,
所以满足条件的c的取值范围为﹣3≤c≤3或11≤c≤17.


科目:初中数学 来源: 题型:
【题目】(1)某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为____元/分钟;
(2)买一个篮球需要m元,买一个排球需要n元,则买3个篮球和5个排球共需要____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;(2)3![]() +(-2
+(-2![]() )+5
)+5![]() +(-8
+(-8![]() );
);
(3)(-103)+(+1![]() )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1![]() );
);
(4)(-2![]() )+(-0.38)+(-
)+(-0.38)+(-![]() )+(+0.38);
)+(+0.38);
(5)(-9![]() )+15
)+15![]() +(-3
+(-3![]() )+(-22.5)+(-15
)+(-22.5)+(-15![]() );
);
(6)[(+![]() )+(-3.5)+(-6)]+[(+2.5)+(+6)+(+
)+(-3.5)+(-6)]+[(+2.5)+(+6)+(+![]() )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.
光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.
(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线;
(2)当⊙O的半径为1时,如图3,
①第一象限内的一条入射光线平行于x轴,且自⊙O的外部照射在其上点P处,此光线经⊙O反射后,反射光线与y轴平行,则反射光线与切线l的夹角为;
②自点A(﹣1,0)出发的入射光线,在⊙O内不断地反射.若第1个反射点P1在第二象限,且第12个反射点P12与点A重合,则第1个反射点P1的坐标为
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.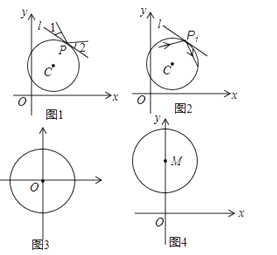
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com