
【题目】计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;(2)3![]() +(-2
+(-2![]() )+5
)+5![]() +(-8
+(-8![]() );
);
(3)(-103)+(+1![]() )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1![]() );
);
(4)(-2![]() )+(-0.38)+(-
)+(-0.38)+(-![]() )+(+0.38);
)+(+0.38);
(5)(-9![]() )+15
)+15![]() +(-3
+(-3![]() )+(-22.5)+(-15
)+(-22.5)+(-15![]() );
);
(6)[(+![]() )+(-3.5)+(-6)]+[(+2.5)+(+6)+(+
)+(-3.5)+(-6)]+[(+2.5)+(+6)+(+![]() )].
)].
【答案】(1)-6.7;(2)-2;(3)-99![]() ;(4)-3;(5)-35;(6)0
;(4)-3;(5)-35;(6)0
【解析】
根据有理数的加法运算律进行运算即可.
解:(1)原式=(0.36+0.3+0.64)+[(-7.4)+(-0.6)].
=1.3-8=-6.7;
(2)3![]() +(-2
+(-2![]() )+5
)+5![]() +(-8
+(-8![]() ).
).
=3![]() +5
+5![]() +
+![]() .
.
=9+(-11).
=-2;
(3)原式=[(-103)+(-97)]+![]() +100.
+100.
=-200+![]() +100=-99
+100=-99![]() ;
;
(4)(-2![]() )+(-0.38)+(-
)+(-0.38)+(-![]() )+(+0.38).
)+(+0.38).
=![]() +[(-0.38)+(+0.38)].
+[(-0.38)+(+0.38)].
=-3+0.
=-3;
(5)原式=[(-9![]() )+(-15
)+(-15![]() )]+[15
)]+[15![]() +(-3
+(-3![]() )]+(-22.5).
)]+(-22.5).
=[(-9)+(-15)+(-![]() )+(-
)+(-![]() )]+[15+(-3)+
)]+[15+(-3)+![]() +(-
+(-![]() )]+(-22.5).
)]+(-22.5).
=-25+12.5+(-22.5).
=-25+[12.5+(-22.5)].
=-25+(-10)=-35;
(6)![]() +[(+2.5)+(+6)+(+
+[(+2.5)+(+6)+(+![]() )].
)].
=(+![]() )+(-3.5)+(-6)+(+2.5)+(+6)+(+
)+(-3.5)+(-6)+(+2.5)+(+6)+(+![]() ).
).
=![]() +[-3.5+(+2.5)]+[(-6)+(+6)].
+[-3.5+(+2.5)]+[(-6)+(+6)].
=1+(-1)+0.
=0.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数x,y在数轴上对应点如图所示:
![]()
(1)在数轴上表示﹣x,|y|;
(2)试把x,y,0,﹣x,|y|这五个数从小到大用“<”号连接,
(3)化简:|x+y|﹣|y﹣x|+|y|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,连接BD,AD=6cm,BD=8cm,∠DBC=90°,现将△AEF沿BD的方向匀速平移,速度为2cm/s,同时,点G从点D出发,沿DC的方向匀速移动,速度为2cm/s.当△AEF停止移动时,点G也停止运动,连接AD,AG,EG,过点E作EH⊥CD于点H,如图2所示,设△AEF的移动时间为t(s)(0<t<4).
(1)当t=1时,求EH的长度;
(2)若EG⊥AG,求证:EG2=AEHG;
(3)设△AGD的面积为y(cm2),当t为何值时,y可取得最大值,并求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
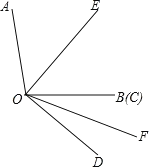
【题目】已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数;
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.
(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
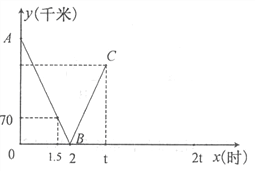
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息:
(1)求线段AB所在直线的函数解析式;
(2) 可求得甲乙两地之间的距离为 千米;
(3)已知两车相遇时快车走了180千米,则快车从甲地到达乙地所需时间为 小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() , 求AE的长.
, 求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,O为坐标原点,点A的坐标为(1,a),点B的坐标为(b,1),点C的坐标为(c,0),其中a、b满足(a+b﹣8)2+|a﹣b+2|=0.
(1)求A、B两点的坐标;
(2)当△ABC的面积为6时,求点C的坐标;
(3)当4≤S△ABC≤10时,求点C的横坐标c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com