
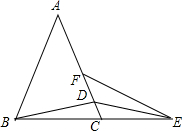
 如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD. 分析 在CD的延长线上取点M,使ED=EM,根据等腰三角形的性质得到∠EDM=∠EMD,由等腰三角形的性质得到∠ABC=∠ACB=∠DCE,∠DBC=∠BED,推出∠ABD=∠M,根据已知条件和邻补角的定义得到∠A=∠MFE,证得△ABD≌△FME,根据全等三角形的性质即可得到结论.
解答 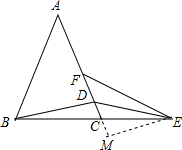 证明:在CD的延长线上取点M,使ED=EM,
证明:在CD的延长线上取点M,使ED=EM,
∴∠EDM=∠EMD,
∵AB=AC,BD=DE,
∴∠ABC=∠ACB=∠DCE,∠DBC=∠BED,
∵∠EDM=∠BED+∠CDE=∠ABC+∠DBE=∠ABD,
∵∠AFE+∠A=180°,∠AFE+∠MFE=180°,
∴∠A=∠MFE,
∵BD=DE=EM,在△ABD与△FME中,$\left\{\begin{array}{l}{∠A=∠EFM}\\{∠ABD=∠FME}\\{BD=EM}\end{array}\right.$,
∴△ABD≌△FME,
∴AD=EF.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
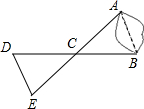 如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.
如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座水房D,在BD的中点C处有一棵百年古树,小明从A出发,沿直线AC一直向前经过点C走到点E(A、C、E三点在同一条直线上),并使CE=CA,然后他测量点E到水房D的距离,则DE的长度就是A、B两点之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
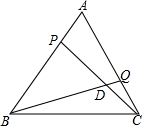 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
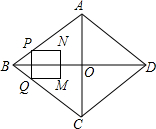 如图,在菱形ABCD中,AB=5cm,AC=6cm,对角线AC、BD相交于点O.动点P从点B出发,沿折线BA-AD以1cm/s的速度向终点D运动,过点P作PQ∥AC交折线BC-CD于点Q,以PQ为边作正方形PQMN,且MN与AC始终在PQ的同侧.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,在菱形ABCD中,AB=5cm,AC=6cm,对角线AC、BD相交于点O.动点P从点B出发,沿折线BA-AD以1cm/s的速度向终点D运动,过点P作PQ∥AC交折线BC-CD于点Q,以PQ为边作正方形PQMN,且MN与AC始终在PQ的同侧.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com