
��ͼ����֪����ABCD�ı߳�AB��2��BC��3����P��AD���ϵ�һ����(P����A��D)��Q��BC���ϵ�����һ�㣮��AQ��DQ����P��PE��DQ��AQ��E����PF��AQ��DQ��F��
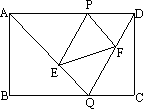
(1)��֤����APE�ס�ADQ��
(2)��AP�ij�Ϊx�������PEF�����S��PEF����x�ĺ�����ϵʽ������P�ںδ�ʱ��S��PEFȡ�����ֵ�����ֵΪ���٣�
(3)��Q�ںδ�ʱ����ADQ���ܳ���С��(�����ȷ��Q�ںδ��Ĺ��̻������ظ���֤��)
 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����DEFG�ڽ���Rt��ABC��D��AB�ϣ�E��F��BC�ϣ�G��AC�ϣ���BAC=90�㣬AB=6cm��AC=8cm��S����DEFG=
��ͼ����֪����DEFG�ڽ���Rt��ABC��D��AB�ϣ�E��F��BC�ϣ�G��AC�ϣ���BAC=90�㣬AB=6cm��AC=8cm��S����DEFG=| 45 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 m/����ٶ��ƶ������M��N����ͬʱ�������ƶ���ʱ��Ϊx�루0��x��6����
m/����ٶ��ƶ������M��N����ͬʱ�������ƶ���ʱ��Ϊx�루0��x��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��A�˶���
��A�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•�����ʼ죩��ͼ����֪Rt��ABC����B=90�㣬AB=8��BC=6����б��ACƽ���ֳ�n�Σ���ÿ��Ϊ�Խ���������AB��BCƽ�е�С���Σ�����ЩС���ε�������ǣ�������
��2012•�����ʼ죩��ͼ����֪Rt��ABC����B=90�㣬AB=8��BC=6����б��ACƽ���ֳ�n�Σ���ÿ��Ϊ�Խ���������AB��BCƽ�е�С���Σ�����ЩС���ε�������ǣ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����ABCD��AB��BC=3��1����A��B��x���ϣ�ֱ��y=mx+n��0��m��n��
��ͼ����֪����ABCD��AB��BC=3��1����A��B��x���ϣ�ֱ��y=mx+n��0��m��n��| 1 |
| 2 |
| 9 |
| 8 |
| 4 |
| 9 |
| 4 |
| 9 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com