
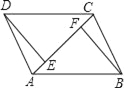
【题目】已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:(1)AF=CE;
(2)AB∥CD;
(3)AD=CB且AD∥CB.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)根据已知条件,利用HL判定Rt△CDE≌Rt△ABF,根据全等三角形的性质即可得AF=CE;(2)由Rt△CDE≌Rt△ABF,即可得∠BAF=∠DCE,根据内错角相等,两直线平行即可得AB∥CD;(3)由AB∥CD,AB=CD,根据一组对边平行且相等的四边形为平行四边形即可判定四边形ABCD是平行四边形,根据平行四边形的性质即可得AD=CB且AD∥CB.
试题解析:
证明:(1)∵DE⊥AC,BF⊥AC,
∴∠CED=∠AFB=90°,
在Rt△CDE和Rt△ABF中,
![]() ,
,
∴Rt△CDE≌Rt△ABF(HL),
∴AF=CE;
(2)∵Rt△CDE≌Rt△ABF,
∴∠BAF=∠DCE,
∴AB∥CD;
(3)∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴AD=CB且AD∥CB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒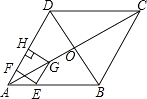
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为;当OO′⊥AD时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:
种类 | 频数 | 频率 |
卡通画 | a |
|
时文杂志 | b | 0.16 |
武侠小说 | 50 | c |
文学名著 | d | e |
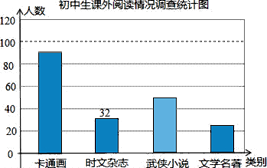
(1)这次随机调查了______名学生,统计表中a=______,d=______;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是______;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D. 
(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
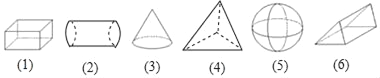
【题目】下列请写出下列几何体,并将其分类.(只填写编号)
如果按“柱”“锥”“球”来分,柱体有_____,椎体有_____,球有_____;
如果按“有无曲面”来分,有曲面的有_____,无曲面的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题: ①若 ![]() >1,则a>b;
>1,则a>b;
②若a+b=0,则|a|=|b|;
③等边三角形的三个内角都相等;
④底角相等的两个等腰三角形全等.
其中原命题与逆命题均为真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB. 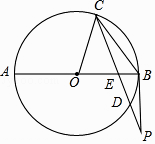
(1)求证:AEEB=CEED;
(2)若⊙O的半径为3,OE=2BE, ![]() =
= ![]() ,求tan∠OBC的值及DP的长.
,求tan∠OBC的值及DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
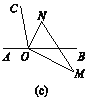
【题目】已知O是直线AB上一点,将一直角三角尺如图QZ-13(a)放置,一直角边ON在直线AB上,另一直角边OM与AB所形成的∠AOM=90°,射线OC在∠AOM内部.
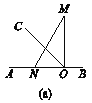

(探究)如图(b),将三角尺绕着点O顺时针旋转,当∠AON=∠CON时,试判断OM是否平分∠BOC,并说明理由.
(拓展)若∠AOC=80°时,三角尺OMN绕O点顺时针旋转一周,每秒旋转5°,则多少秒后,∠MOC=∠MOB?
(延伸)在上述条件下,如图(c),旋转三角尺使ON在∠BOC内部,另一边OM在直线AB的另一侧,下面两个结论:①∠NOC-∠BOM的值不变;②∠NOC+∠BOM的值不变.选择其中一个正确的结论说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com