
【题目】如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB. 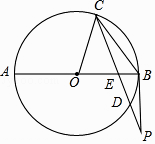
(1)求证:AEEB=CEED;
(2)若⊙O的半径为3,OE=2BE, ![]() =
= ![]() ,求tan∠OBC的值及DP的长.
,求tan∠OBC的值及DP的长.
【答案】
(1)证明:连接AD,
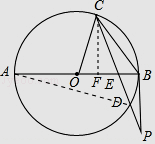
∵∠A=∠BCD,∠AED=∠CEB,
∴△AED∽△CEB,
∴ ![]() =
= ![]() ,
,
∴AEEB=CEED;
(2)解:∵⊙O的半径为3,
∴OA=OB=OC=3,
∵OE=2BE,
∴OE=2,BE=1,AE=5,
∵ ![]() =
= ![]() ,
,
∴设CE=9x,DE=5x,
∵AEEB=CEED,
∴5×1=9x5x,
解得:x1= ![]() ,x2=﹣
,x2=﹣ ![]() (不合题意舍去)
(不合题意舍去)
∴CE=9x=3,DE=5x= ![]() ,
,
过点C作CF⊥AB于F,

∵OC=CE=3,
∴OF=EF= ![]() OE=1,
OE=1,
∴BF=2,
在Rt△OCF中,
∵∠CFO=90°,
∴CF2+OF2=OC2,
∴CF=2 ![]() ,
,
在Rt△CFB中,
∵∠CFB=90°,
∴tan∠OBC= ![]() =
= ![]() =
= ![]() ,
,
∵CF⊥AB于F,
∴∠CFB=90°,
∵BP是⊙O的切线,AB是⊙O的直径,
∴∠EBP=90°,∴∠CFB=∠EBP,
在△CFE和△PBE中
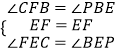 ,
,
∴△CFE≌△PBE(ASA),
∴EP=CE=3,
∴DP=EP﹣ED=3﹣ ![]() =
= ![]() .
.
【解析】(1)直接根据题意得出△AED∽△CEB,进而利用切线的性质的出答案;(2)利用已知得出EC,DE的长,再利用勾股定理得出CF的长,t即可得出an∠OBC的值,再利用全等三角形的判定与性质得出DP的长.
【考点精析】根据题目的已知条件,利用切线的性质定理和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;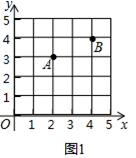
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.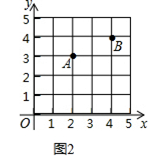
查看答案和解析>>
科目:初中数学 来源: 题型:
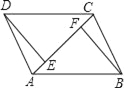
【题目】已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:(1)AF=CE;
(2)AB∥CD;
(3)AD=CB且AD∥CB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )

A. 120°B. 135°C. 145°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3. 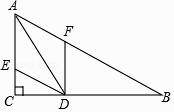
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是50
B.众数是51
C.方差是42
D.极差是21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例). 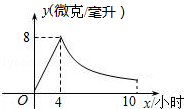
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73) 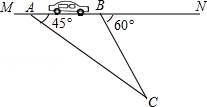
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( ) 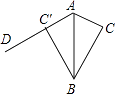
A.3
B.4
C.5.5
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com