（1）（-8）-47+18-（-27）
（2）计算：（-3）×（-9）－8×（-5）
（3）计算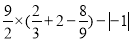
（4） 计算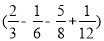
×（－24）
（5）计算12÷（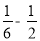
）+2×
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案科目：初中数学 来源：2016届山西省九年级素质检测数学试卷（解析版） 题型：解答题
小美周末来到公园，发现在公园一角有一种“守株待兔”游戏。游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的。规定：①玩家只能将小兔从A、B两个出入口放入；
②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值5元小兔玩具，否则应付费3元。
（1）、问小美得到小兔玩具的机会有多大？
（2）、假设有100人次玩此游戏，估计游戏设计者可赚多少元？
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省威海市七年级上期中数学试卷（解析版） 题型：解答题
问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成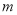
种不同的等腰三角形，为探究m与n之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
（1）用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当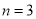
时，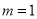
（2）用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当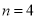
时，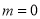
（3）用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当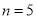
时，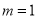
（4）用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当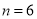
时，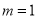
综上所述，可得表①
| 3 | 4] | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二：
（1）用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
（2）分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三
角形？（只需把结果填在表②中）
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用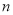
根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
（设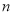
分别等于
、
、
、
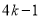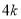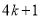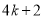，其中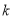
是整数，把结果填在表③中）
|
|
|
|
|
|
问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省威海市七年级上期中数学试卷（解析版） 题型：选择题
如图，△ABC中，AB＝AC，∠A＝36°，BD是AC边上的高，则∠DBC的度数是（ ）
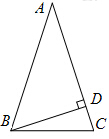
A．18° B．24° C．30° D．36°
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省威海市六年级上期中数学试卷（解析版） 题型：解答题
某检修小组乘汽车检修公路道路。向东记为正，向西记为负。某天自A地出发。所走路程（单位：千米）为：+22，-3，+4，-2，-8，-17，-2，+12，+7，-5；
问：①，最后他们是否回到出发点？若没有，则在A地的什么地方？距离A地多远？
②，若每千米耗油0.05升，则今天共耗油多少升？
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省威海市六年级上期中数学试卷（解析版） 题型：填空题
在下边的展开图中，分别填上数字1，2，3，4，5，6，使得折叠成正方体后，相对面上的数字之和相等，则a= ，b= ，c= ．
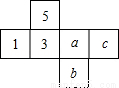
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省威海市六年级上期中数学试卷（解析版） 题型：选择题
数6，-1，15，-3中，任取三个不同的数相加，其中和最小的是（ ）
A、-3 B、-1 C、3 D、2
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省威海市八年级上期中数学试卷（解析版） 题型：填空题
已知关于x的分式方程 ＝-1的解是非正数，则a的取值范围是_____________．
查看答案和解析>>
科目：初中数学 来源：2015-2016学年山东省七年级下第一次月考数学试卷（解析版） 题型：填空题
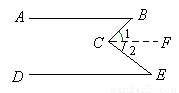
如图， AB∥DE，试问∠B、∠E、∠BCE有什么关系．
∠B＋∠E＝∠BCE
过点C作CF∥AB，
则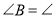
1 （ ）
又∵AB∥DE，AB∥CF，
∴____________（ ）
∴∠E＝∠____（ ）
∴∠B＋∠E＝∠1＋∠2
即∠B＋∠E＝∠BCE．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
