
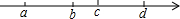 ��ͼ��a��b��c��d�������ϵ�λ����ͼ��ʾ����b-c=-4��
��ͼ��a��b��c��d�������ϵ�λ����ͼ��ʾ����b-c=-4������ ��1����b-c=-4���ó�����ұߵø����ұ�ȥ��ߵ�������Ͼ���ֵ�����廯�ɣ�
��2����bc��0���ó�a��b��0��c��d����һ�����þ���ֵ�������Ȼ����ٽ�һ���ϲ����ɣ�
��3������˶�ʱ��Ϊt���ֱ��ʾ��P��Q��M��N�ĵ��ʾ��������һ����ͣ����a+2b+d=0���жϵó��𰸼��ɣ�
��� �⣺��1����b-c=-4��
���|a-c|=c-a����|d-b|=d-b����|c-b|=c-b��
��2����bc��0��
��a��b��0��c��d��
��|a+b|-|b+d|+|c+d|-|a+c|=-a-b-b-d+c+d-a+c=-2a-2b+2c��
��3�����˶�ʱ��Ϊt��
��P=a-5t��Q=b-2t��M=c+3t��N=c+4t��
��a-5t+b-2t+c+3t+d+4t=a+b+c+d��
��a+2b+d=0��b-c=-4��
��a+b+c+d=-2b+b+c=-��b-c��=4��
��P��Q��M��N�ĵ��ʾ�����ĺͲ������仯���������4��
���� ���⿼����ʽ�ļӼ�������㣬����ֵ�����壬���þ���ֵ�����廯���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2y+xy2=x3y3 | B�� | 9ab-ba=10ba | C�� | 2a2-a2=2 | D�� | xy2-2xy2=-xy2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����Rt��ABC�У���֪��A=90�㣬AB=6��BC=8cm��DE��ֱƽ��BC����BE�ij��ǣ�������
��ͼ��ʾ����Rt��ABC�У���֪��A=90�㣬AB=6��BC=8cm��DE��ֱƽ��BC����BE�ij��ǣ�������| A�� | 3cm | B�� | 4cm | C�� | 5cm | D�� | ���ϴ𰸶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ⲻ��ʽ�飺$\left\{\begin{array}{l}{3x-1��2��x+1����}\\{\frac{x+3}{2}��1��}\end{array}\right.$�����������������ϱ�ʾ����⼯��
�ⲻ��ʽ�飺$\left\{\begin{array}{l}{3x-1��2��x+1����}\\{\frac{x+3}{2}��1��}\end{array}\right.$�����������������ϱ�ʾ����⼯���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ�ǡ�ABC�У���C=90�㣬AC=4��BC=3��D��AC���е㣬��E��AB���ϵ�һ���㣬��F������BC��һ���㣬�ҡ�FDE=90�㣬��AE=x��CF=y��
��ͼ����ֱ�ǡ�ABC�У���C=90�㣬AC=4��BC=3��D��AC���е㣬��E��AB���ϵ�һ���㣬��F������BC��һ���㣬�ҡ�FDE=90�㣬��AE=x��CF=y���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
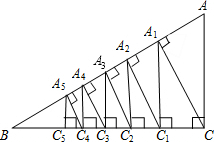 ��ͼ����Rt��BCA�У���C=90�㣬AC=3��BC=4������C��CA1��AB������Ϊ��A1���ٹ���A1��A1C1��BC������Ϊ��C1���������ϵķ�����������ȥ���õ�Rt��A5C5C4�����߶�A5C5�ij���
��ͼ����Rt��BCA�У���C=90�㣬AC=3��BC=4������C��CA1��AB������Ϊ��A1���ٹ���A1��A1C1��BC������Ϊ��C1���������ϵķ�����������ȥ���õ�Rt��A5C5C4�����߶�A5C5�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
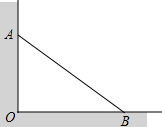 ��ͼ��ʾ���ڽ��������ϣ�Ϊ��֧��һ��ǽ����һ��5m��ľ�ģ����˳���ǽ�ϣ��˳��ڵ����ϣ�ͼ��OB=4m������Ϊ������֧�ŵ�Ч��������ǰ�ƣ����������ƣ����ƶ�������ȣ���Ӧ�ƶ������ף�
��ͼ��ʾ���ڽ��������ϣ�Ϊ��֧��һ��ǽ����һ��5m��ľ�ģ����˳���ǽ�ϣ��˳��ڵ����ϣ�ͼ��OB=4m������Ϊ������֧�ŵ�Ч��������ǰ�ƣ����������ƣ����ƶ�������ȣ���Ӧ�ƶ������ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com