
【题目】已知:如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC. 
(1)求证:BE=DG;
(2)若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD.
∵AE是BC边上的高,且CG是由AE沿BC方向平移而成.
∴CG⊥AD.
∴∠AEB=∠CGD=90°.
∵AE=CG,
∴Rt△ABE≌Rt△CDG(HL).
∴BE=DG;
(2)解:当BC= ![]() AB时,四边形ABFG是菱形.
AB时,四边形ABFG是菱形.
证明:∵AB∥GF,AG∥BF,
∴四边形ABFG是平行四边形.
∵Rt△ABE中,∠B=60°,
∴∠BAE=30°,
∵BC= ![]() AB
AB
∴BE=CF
∴EF= ![]() AB
AB
∴AB=BF
∴四边形ABFG是菱形
【解析】(1)根据平移的性质,可得:BE=FC,再证明Rt△ABE≌Rt△CDG可得:BE=DG;(2)要使四边形ABFG是菱形,须使AB=BF;根据条件找到满足AB=BF的AB与BC满足的数量关系即可.
【考点精析】利用平行四边形的性质和菱形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注,某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度,对该校部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为A类(非常喜欢),B类(较喜欢),C类(一般),D类(不喜欢),请结合两幅统计图,回答下列问题
(1)写出本次抽样调查的样本容量;
(2)请补全两幅统计图;
(3)若该校有2000名学生.请你估计观看“中国汉字听写大会”节目不喜欢的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息,下列说法正确的个数为( ) (1 )甲登山上升的速度是每分钟10米;(2)乙在A地时距地面的高度b为30米;(3)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,乙登山1分钟时,距地面的高度为15米;(4)登山时间为4分钟,9分钟,15分钟时,甲、乙两人距地面的高度差为50米.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.
(1)求证:AB=AC;
(2)填空:①若AB=6,CD=4,则BC=;
②连接OD,当∠A的度数为时,四边形ODEB是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图: 第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )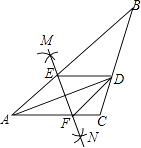
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称
与y轴相交于点A,点B与点O关于点A对称
(1)填空:点B的坐标是;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由;
(3)在(2)的条件下,若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=k(x+1)(x﹣ ![]() )与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形抛物线的条数是( )
)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形抛物线的条数是( )
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=2 ![]() ,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1 , 矩形PDFE的面积为S2 , y=S1+S2 , 则y与x的关系式是 .
,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1 , 矩形PDFE的面积为S2 , y=S1+S2 , 则y与x的关系式是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年3月31日是全国中小学生安全教育日,某校全体学生参加了“珍爱生命,预防溺水”专题活动,学习了游泳“五不准”,为了了解学生对“五不准”的知晓情况,随机抽取了200名学生作调查,请根据下面两个不完整的统计图解答问题: 
(1)求在这次调查中,“能答5条”人数的百分比和“仅能答3条”的人数;
(2)若该校共有2000名学生,估计该校能答3条不准以上(含3条)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com