
分析 首先根据一元二次方程mx2+nx+1=0有两个相等的实数根得到n2=4m,然后把n2=4m代入$\frac{{mn}^{2}}{(m-2)^{2}+{n}^{2}-4}$化简求值即可.
解答 解:∵一元二次方程mx2+nx+1=0有两个相等的实数根,
∴△=n2-4m=0,
∴n2=4m,
∴$\frac{{mn}^{2}}{(m-2)^{2}+{n}^{2}-4}$=$\frac{4{m}^{2}}{(m-2)^{2}+4m-4}$=$\frac{4{m}^{2}}{{m}^{2}}$=4.
点评 本题主要考查了根的判别式的知识,解答本题要掌握一元二次方程根的情况与判别式△的关系△=0?方程有两个相等的实数根,此题难度不大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
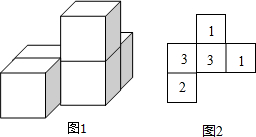 (1)如图1所示,是用五个小正方体搭成的几何体,请画出它的三视图.
(1)如图1所示,是用五个小正方体搭成的几何体,请画出它的三视图. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
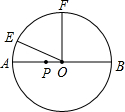 已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )| A. | 5cm | B. | 5$\sqrt{2}$cm | C. | 5$\sqrt{3}$cm | D. | 10cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com