
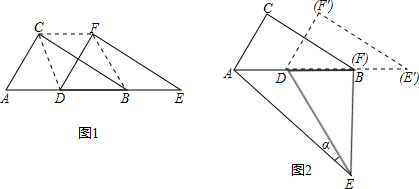
���� ��1������ƽ�Ƶ����ʵõ�AD=BE���ٽ������ƽ����ľ�����ȣ���������ACD���������������BEF�����������Ҫ������ε��������������ABC�����������60�ȵ�ֱ��������ABC��AC=1���������BC�ij����Ӷ�����������
��2����D����DH��AE��H������Ҫ��Ľǹ��쵽ֱ���������У�����������ADE������IJ�ͬ���㷽�����������DH�ij���������⣮
��� �⣺��1����Rt��ABC�У�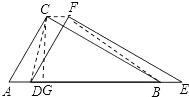
�ߡ�A=60�㣬AC=1��
��BC=$\sqrt{3}$��
��S����CDBF=S��ABC=$\frac{\sqrt{3}}{2}$��
�ʴ�Ϊ��$\frac{\sqrt{3}}{2}$��
��2����D����DH��AE��H����Rt��ABE��AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{7}$��
�ߡ�DAH=��EAB����DHA=��ABE=90�㣬
���ADH�ס�AEB��$\frac{DH}{BE}=\frac{AD}{AE}$����$\frac{DH}{\sqrt{3}}=\frac{1}{\sqrt{7}}$�����DH=$\frac{\sqrt{21}}{7}$��
��DE=AB=2����Rt��DHE�У�sin�Ϧ�=$\frac{DH}{DE}$=$\frac{\sqrt{21}}{7}$��2=$\frac{\sqrt{21}}{14}$��
�ʴ�Ϊ��$\frac{\sqrt{21}}{14}$��
���� �ۺ�����ֱ�������ε����ʺ�ƽ�Ƶ����ʽ��з������㣬����ѧ���ۺ�������ѧ֪ʶ��������������һ���������⣬��Ȼͼ�η����˱仯��������ͬ��ͬ�ȸߵ������������ȣ��ҵ������ȵ��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{b-a}{a}$ | B�� | $\frac{a-b}{a}$ | C�� | -1 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�ı���ֽƬABCD���ֽ���ֽƬ��ƴ��һ�����������ȵ�ƽ���ı���ֽƬ��������ü���������������ܷ��������ܣ��á��ܡ����ܡ���գ��������ܡ�����ȷ���ü��ߵ�λ�ã���˵��ƴ�ӷ�����������ܡ������Ҫ˵�����ɣ����������ɣ�ȡ�ı���ֽƬABCD���ߵ��е�E��F��G��H������EG��FH����EG��FHΪ�ü��ߣ���2��H��ת180�㡢4��G��ת180�㣬4��BD����ƽ�ƣ�ʹB��D�غϣ�
��ͼ����֪�ı���ֽƬABCD���ֽ���ֽƬ��ƴ��һ�����������ȵ�ƽ���ı���ֽƬ��������ü���������������ܷ��������ܣ��á��ܡ����ܡ���գ��������ܡ�����ȷ���ü��ߵ�λ�ã���˵��ƴ�ӷ�����������ܡ������Ҫ˵�����ɣ����������ɣ�ȡ�ı���ֽƬABCD���ߵ��е�E��F��G��H������EG��FH����EG��FHΪ�ü��ߣ���2��H��ת180�㡢4��G��ת180�㣬4��BD����ƽ�ƣ�ʹB��D�غϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
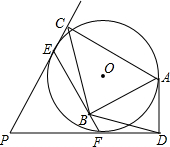 ��ͼ��PE��PF�ֱ����O������E��F���㣬AΪ��O�ϲ�ͬ��E��F�ĵ㣬AB��EF��B��AC��PE��C��AD��PF��D����֤����ACB=��ABD��
��ͼ��PE��PF�ֱ����O������E��F���㣬AΪ��O�ϲ�ͬ��E��F�ĵ㣬AB��EF��B��AC��PE��C��AD��PF��D����֤����ACB=��ABD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
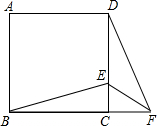 ��ͼ����������ABCD�У�EΪDC���ϵĵ㣬����BE������BCE�Ƶ�C��˳ʱ�뷽����ת90��õ���DCF������EF�����EFC�Ķ���Ϊ��������
��ͼ����������ABCD�У�EΪDC���ϵĵ㣬����BE������BCE�Ƶ�C��˳ʱ�뷽����ת90��õ���DCF������EF�����EFC�Ķ���Ϊ��������| A�� | 25�� | B�� | 30�� | C�� | 45�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
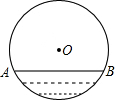 ��ͼ��ˮƽ����һ���������ֱ��Ϊ100cm�������Ͳ��������ABΪ80cm�����������Ͳ��ֵ������Ϊ20cm��
��ͼ��ˮƽ����һ���������ֱ��Ϊ100cm�������Ͳ��������ABΪ80cm�����������Ͳ��ֵ������Ϊ20cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com