
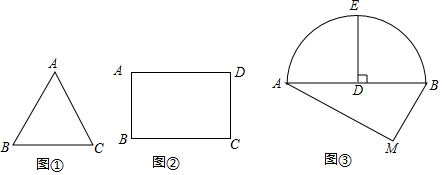
分析 (1)构建Rt△AOD中,利用cos∠OAD=cos30°=$\frac{AD}{OA}$,可得OA的长;
(2)经过矩形对角线交点的直线将矩形面积平分,根据此结论作出PQ,利用勾股定理进行计算即可;
(3)如图3,作辅助线,先确定圆心和半径,根据勾股定理计算半径:
在Rt△AOD中,r2=122+(r-8)2,解得:r=13根据三角形面积计算高MN的长,证明△ADC∽△ANM,列比例式求DC的长,确定点O在△AMB内部,利用勾股定理计算OM,则最大距离FM的长可利用相加得出结论.
解答 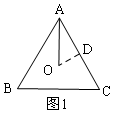 解:(1)如图1,过O作OD⊥AC于D,则AD=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6,
解:(1)如图1,过O作OD⊥AC于D,则AD=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6,
∵O是内心,△ABC是等边三角形,
∴∠OAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,
在Rt△AOD中,cos∠OAD=cos30°=$\frac{AD}{OA}$,
∴OA=6÷$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$;
(2)存在,如图2,连接AC、BD交于点O,连接PO并延长交BC于Q,则线段PQ将矩形ABCD的面积平分,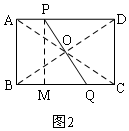
∵点O为矩形ABCD的对称中心,
∴CQ=AP=3,
过P作PM⊥BC于点,则PM=AB=12,MQ=18-3-3=12,
由勾股定理得:PQ=$\sqrt{P{M}^{2}+M{Q}^{2}}$=$\sqrt{1{2}^{2}+1{2}^{2}}$=12$\sqrt{2}$;
(3)如图3,作射线ED交AM于点C
∵AD=DB,ED⊥AB,$\widehat{AB}$是劣弧,
∴$\widehat{AB}$所在圆的圆心在射线DC上,
假设圆心为O,半径为r,连接OA,则OA=r,OD=r-8,AD=$\frac{1}{2}$AB=12,
在Rt△AOD中,r2=122+(r-8)2,
解得:r=13,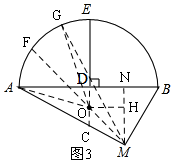
∴OD=5,
过点M作MN⊥AB,垂足为N,
∵S△ABM=96,AB=24,
∴$\frac{1}{2}$AB•MN=96,
$\frac{1}{2}$×24×MN=96,
∴MN=8,NB=6,AN=18,
∵CD∥MN,
∴△ADC∽△ANM,
∴$\frac{DC}{MN}=\frac{AD}{AN}$,
∴$\frac{DC}{8}=\frac{12}{18}$,
∴DC=$\frac{16}{3}$,
∴OD<CD,
∴点O在△AMB内部,
∴连接MO并延长交$\widehat{AB}$于点F,则MF为草坪上的点到M点的最大距离,
∵在$\widehat{AB}$上任取一点异于点F的点G,连接GO,GM,
∴MF=OM+OF=OM+OG>MG,
即MF>MG,
过O作OH⊥MN,垂足为H,则OH=DN=6,MH=3,
∴OM=$\sqrt{M{H}^{2}+O{H}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴MF=OM+r=3$\sqrt{5}$+13≈19.71(米),
答:喷灌龙头的射程至少为19.71米.
点评 本题是圆的综合题,考查了三角形相似的性质和判定、勾股定理、等边三角形的性质及内心的定义、特殊的三角函数值、矩形的性质等知识,明确在特殊的四边形中将面积平分的直线一定过对角线的交点,本题的第三问比较复杂,辅助线的作出是关键,根据三角形的三角关系确定其最大射程为MF.


科目:初中数学 来源: 题型:填空题
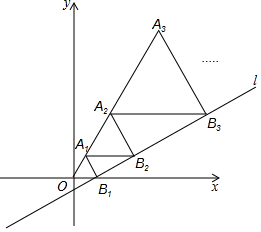 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
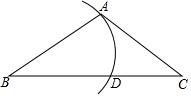 如图,则△ABC中,∠BAC=100°,AB=AC=4,以点B为圆心,BA长为半径作圆弧,交BC于点D,则$\widehat{AD}$的长为$\frac{8π}{9}$.(结果保留π)
如图,则△ABC中,∠BAC=100°,AB=AC=4,以点B为圆心,BA长为半径作圆弧,交BC于点D,则$\widehat{AD}$的长为$\frac{8π}{9}$.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | C. | $\frac{x-y}{x+y}$ | D. | x2+y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) |
| 羽毛球 | 30 |
| 篮球 | a |
| 乒乓球 | 36 |
| 排球 | b |
| 足球 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象过点(1,0) | B. | y值随着x值增大而减小 | ||
| C. | 它的图象经过第二象限 | D. | 当x>1时,y>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com