
【题目】如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC. 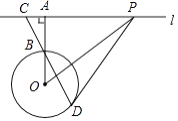
(1)求证:PD是⊙O的切线;
(2)若AC=1,AB=2,PD=6,求⊙O的半径r和△PCD的面积.
【答案】
(1)解:连接OD,
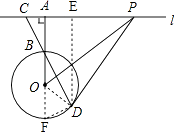
∴∠ABC=∠OBD=∠ODB,
∵OA⊥l,
∴∠PCD+∠ABC=90°,
∴∠PCD+∠ODB=90°,
∵∠PCD=∠PDC,
∴∠PDC+∠ODB=90°,即∠ODP=90°,
∴PD是⊙O的切线;
(2)解:∵∠PCD=∠PDC,
∴PC=PD=6,
∴PA=5,
设OB=OF=OD=r,
由PA2+AO2=PD2+OD2可得52+(2+r)2=62+r2,
解得:r= ![]() ,
,
延长AO交⊙O于点F,连接DF,
∵∠ABC=∠DBF、∠BAC=∠BDF=90°,
∴△ABC∽△DBF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DB= ![]() ,
,
过点D作DE⊥PC于点E,
∴△CAB∽△CED,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:DE= ![]() ,
,
∴S△PCD= ![]() PCDE=
PCDE= ![]() ×6×
×6× ![]() =
= ![]() .
.
【解析】(1)连接OD,知∠ABC=∠OBD=∠ODB,由∠PCD+∠ABC=90°知∠PCD+∠ODB=90°,结合∠PCD=∠PDC可得∠ODP=90°,即可得证;(2)由∠PCD=∠PDC知PC=PD=6、PA=5,根据PA2+AO2=PD2+OD2可得r= ![]() ;延长AO交⊙O于点F,连接DF,证△ABC∽△DBF得
;延长AO交⊙O于点F,连接DF,证△ABC∽△DBF得 ![]() =
= ![]() ,即可知DB=
,即可知DB= ![]() ,作DE⊥PC于点E,由△CAB∽△CED知
,作DE⊥PC于点E,由△CAB∽△CED知 ![]() =
= ![]() ,求得DE=
,求得DE= ![]() ,从而求得△PCD的面积.
,从而求得△PCD的面积.
【考点精析】利用切线的判定定理对题目进行判断即可得到答案,需要熟知切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】按要求画图,并回答问题:
如图,在同一平面内有三点A,B,C.

(1)画直线AC;
(2)画射线CB;
(3)过点B作直线AC的垂线BD,垂足为D;
(4)画线段AB及线段AB的中点E,连接DE;
(5)通过画图和测量,与线段DE长度相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,C是劣弧 ![]() 的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2. 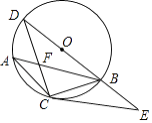
(1)求CB的长;
(2)延长DB到E,使BE=OB,连接CE,求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为m(结果保留根号)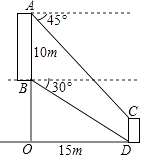
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划从本地向甲、乙两地运送海产品进行销售.本地与甲、乙两地都有铁路和公路相连(如图所示),铁路的单位运价为2元/(吨千米),公路的单位运价为3元/(吨千米) 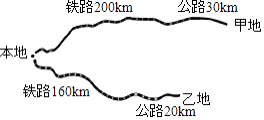
(1)若公司计划往甲、乙两地运输海产品共需铁路运费3680元,公路运费780元,求计划从本地向甲乙两地运输海产品各多少吨?
(2)经市场调查发现,甲地海产品的实际需求量比计划减少a(a>0)吨,但运到甲、乙两地的总量不变,且运到甲地的海产品不少于运到乙地的海产品,当a为多少时,实际总运费w最低?最低总运费是多少? (参考公式:货运运费=单位运价×运输里程×货物重量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 在
在![]() 的
的![]() 边上,
边上,![]() ,
,![]() ,为了判断
,为了判断![]() 与
与![]() 的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
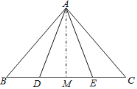
解:作![]() ,垂足为
,垂足为![]()
∵![]() ,
,
∴![]() 是________三角形,
是________三角形,
∴![]() ________
________
又∵![]() ,
,
∴![]() ________,即
________,即![]() ________;
________;
又∵________(自己所作),
∴![]() 是线段________的垂直平分线;
是线段________的垂直平分线;
∴![]() ________
________
∴________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
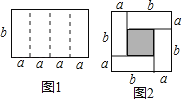
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=5,xy=4,求x﹣y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com