
【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
【答案】
(1)解:四边形ABCD是矩形.理由如下:
∵AC与BD是圆的直径,
∴∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,
∴四边形ABCD是矩形;
(2)解:证明:∵BO=CO,
又∵BE⊥AC于E,CF⊥BD于F,
∴∠BEO=∠CFO=90°.
在△BOE和△COF中, 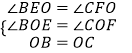 ,
,
∴△BOE≌△COF(AAS).
∴BE=CF.
【解析】(1)由圆周角定理得出∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,即可得出四边形ABCD是矩形;(2)由AAS证明△BOE≌△COF,得出对应边相等即可.
【考点精析】根据题目的已知条件,利用矩形的判定方法和圆周角定理的相关知识可以得到问题的答案,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
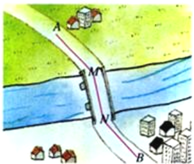
【题目】如图,A 和 B 两地在一条河的两岸,现要在河上造一座桥 MN.桥造在何处才能使从 A 到 B 的路径 AMNB 最短?在下图中画出路径,不写画法但要说明理由.(假定河的两岸是平行的直线,桥要与河垂直.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC. 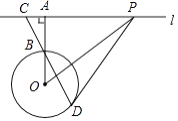
(1)求证:PD是⊙O的切线;
(2)若AC=1,AB=2,PD=6,求⊙O的半径r和△PCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式 12=1= ![]() ×1×2×(2+1)
×1×2×(2+1)
12+22= ![]() ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ![]() ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ![]() ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
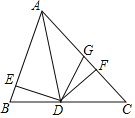
【题目】如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y= ![]() x+4,与x轴相交于点D.
x+4,与x轴相交于点D.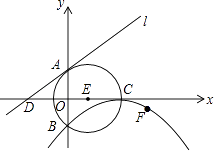
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com