
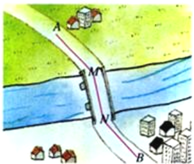
【题目】如图,A 和 B 两地在一条河的两岸,现要在河上造一座桥 MN.桥造在何处才能使从 A 到 B 的路径 AMNB 最短?在下图中画出路径,不写画法但要说明理由.(假定河的两岸是平行的直线,桥要与河垂直.)
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律.如图是2018年12月份的日历,我们任意选择其中所示的十字形部分,将每个部分中间数的左右两数,上下两数分别相乘,再把所得的结果相减.
(1)计算:11×13-5×19;16×18–10×24;(直接写结果)
(2)请你用整式的运算对以上的规律加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室需要一批无盖的长方体模型,一张大纸板可以做成长方体的侧面30个,或长方体的底面25个,一个无盖的长方体由4个侧面和一个底面构成. 现有26张大纸板,则用多少张做侧面,多少张做底面才可以使得刚好配套,没有剩余?
反思:应用二元一次方程组解应用题时,要注意解题的步骤,解、设、答一个不能少,而由于未知数有两个,则必须根据题意找出两个等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图,并回答问题:
如图,在同一平面内有三点A,B,C.

(1)画直线AC;
(2)画射线CB;
(3)过点B作直线AC的垂线BD,垂足为D;
(4)画线段AB及线段AB的中点E,连接DE;
(5)通过画图和测量,与线段DE长度相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,A1B的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 ![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.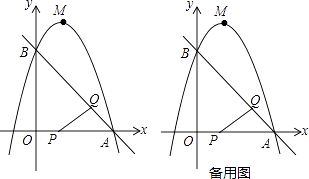
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,C是劣弧 ![]() 的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2. 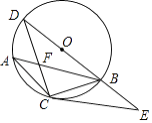
(1)求CB的长;
(2)延长DB到E,使BE=OB,连接CE,求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com