
【题目】如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
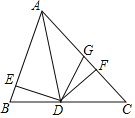
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
(1)根据角平分线的性质可得出DE=DF,结论(1)正确;
(2)由DE=DF、∠BED=∠GFD、BD=GD可证出△BDE≌△GDF(HL),根据全等三角形的性质可得出∠B=∠DGF,结论(2)正确;
(3)利用全等三角形的判定定理AAS可证出△ADE≌△ADF,由此可得出AE=AF,根据△BDE≌△GDF可得出BE=GF,结合AB=AE+EB即可得出AB=AF+FG,结论(3)不正确;
(4)根据全等三角形的性质可得出S△ADE=S△ADF、S△BDE=S△GDF,结合S△ABD=S△ADE+S△BDE=50、S△ADG=S△ADF-S△GDF=38可求出△DFG的面积是6,结论(4)不正确.综上即可得出结论.
(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,结论(1)正确;
(2)在△BDE和△GDF中,![]() ,
,![]()
∴△BDE≌△GDF(HL),
∴∠B=∠DGF,结论(2)正确;
(3)在△ADE和△ADF中,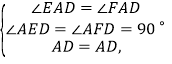
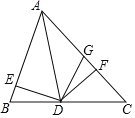
∴△ADE≌△ADF(AAS),
∴AE=AF.
∵△BDE≌△GDF,
∴BE=GF,
∴AB=AE+EB=AF+FG,结论(3)不正确;
(4)∵△ADE≌△ADF,△BDE≌△GDF,
∴![]()
∵![]()
∴![]() ,结论(4)不正确。
,结论(4)不正确。
综上所述:正确的结论有(1)(2).
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为m(结果保留根号)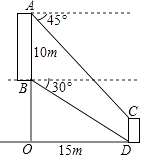
查看答案和解析>>
科目:初中数学 来源: 题型:
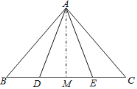
【题目】已知点![]() 、
、![]() 在
在![]() 的
的![]() 边上,
边上,![]() ,
,![]() ,为了判断
,为了判断![]() 与
与![]() 的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
解:作![]() ,垂足为
,垂足为![]()
∵![]() ,
,
∴![]() 是________三角形,
是________三角形,
∴![]() ________
________
又∵![]() ,
,
∴![]() ________,即
________,即![]() ________;
________;
又∵________(自己所作),
∴![]() 是线段________的垂直平分线;
是线段________的垂直平分线;
∴![]() ________
________
∴________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式:
月使用费 | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.20 | 免费 |
方式二 | 100 | 380 | 0.25 | 免费 |
(月使用费固定收;主叫不超过限定的时间不再收费,主叫超过限定时间的部分加收超时费;被叫免费)
(1)若张聪某月主叫通话时间为200分钟,则他按方式一计费需____元,按方式二计费需____
元;李华某月按方式二计费需107元,则李华该月主叫通话时间为_____分钟;
(2)是否存在某主叫通话时间![]() (分钟),按方式一和方式二的计费相等?若存在,请求出
(分钟),按方式一和方式二的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)直接写出当月主叫通话时间![]() (分钟)满足什么条件时,选择方式一省钱。
(分钟)满足什么条件时,选择方式一省钱。
查看答案和解析>>
科目:初中数学 来源: 题型:
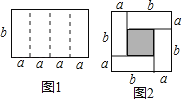
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=5,xy=4,求x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
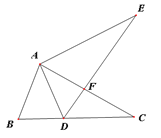
【题目】如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,∠BAD=∠CAE,AC=AE.
(1)求证:△ABC≌△ADE;
(2)若∠B=60°,求证:△ABD是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
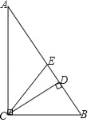
【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,以下判断中正确的个数有( )
①∠DCB=∠A;②∠DCB=∠ACE;③∠ACD=∠BCE;④∠BCE=∠BEC.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com