练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

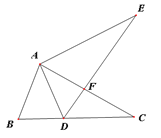
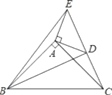
    【题目】如图，点E在△ABC外部，点D在BC边上，DE交AC于点F，若∠C=∠E，∠BAD=∠CAE，AC=AE．

    （1）求证：△ABC≌△ADE；

    （2）若∠B=60°，求证：△ABD是等边三角形．

    【答案】（1）证明见解析；（2）证明见解析

    【解析】

    （1）根据已知求得∠BAC＝∠DAE，再由已知∠E＝∠C，AE＝AC，所以根据ASA可判定△ABC≌△ADE；

    （2）由全等三角形对应边相等得到AB=AD，再由有一个角为60°的等腰三角形是等边三角形即可得到结论．

    （1）∵∠1＝∠2，∴∠1+∠DAC＝∠2+∠DAC，即∠BAC＝∠DAE．

    在△ABC和△ADE中，∵，∴△ABC≌△ADE（ASA）．

    （2）∵△ABC≌△ADE，∴AB=AD．

    ∵∠B=60°，∴△ABD是等边三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，过原点的直线y=k1x和y=k2x与反比例函数y= 的图象分别交于两点A，C和B，D，连接AB，BC，CD，DA．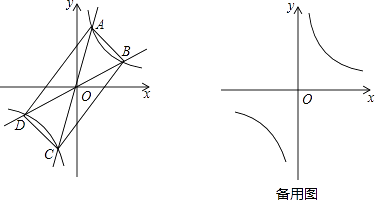

    （1）四边形ABCD一定是四边形；（直接填写结果）
    （2）四边形ABCD可能是矩形吗？若可能，试求此时k1 ， k2之间的关系式；若不能，说明理由；
    （3）设P（x1 ， y1），Q（x2 ， y2）（x2＞x1＞0）是函数y= 图象上的任意两点，a= ，b= ，试判断a，b的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

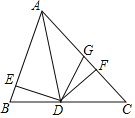
    【题目】如图，已知AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BD=DG．

    下列结论：（1）DE=DF；（2）∠B=∠DGF； （3）AB＜AF+FG；（4）若△ABD和△ADG的面积分别是50和38，则△DFG的面积是8．其中一定正确的有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论： ①a＜0；②c＞0；③b2﹣4ac＞0；④ ＜0中，正确的结论有（ ）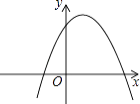

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】填空，完成下列说理过程

    如图，∠AOB＝90°，∠COD＝90°，OA平分∠DOE，若∠BOC＝20°，求∠COE的度数

    解：因为∠AOB＝90°．

    所以∠BOC+∠AOC＝90°

    因为∠COD＝90°

    所以∠AOD+∠AOC＝90°．

    所以∠BOC＝∠AOD． （　 　）

    因为∠BOC＝20°．

    所以∠AOD＝20°．

    因为OA平分∠DOE

    所以∠　 　＝2∠AOD＝　 　°． （　 　）

    所以∠COE＝∠COD﹣∠DOE＝　 　°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）小明做作业时，不小心将方程中●的一个常数污染了看不清楚，怎么办呢？

    （1）小红告诉他该方程的解是x＝3．那么这个常数应是多少呢？

    （2）小芳告诉他该方程的解是负数，并且这个常数是负整数，请你试求该方程的解．（友情提醒：设这个常数为m.）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列例题

    解方程：|x|+|2x﹣1|＝5．

    解：①当x≥0.5时，原方程可化为：x+2x﹣1＝5，它的解是x＝2；

    ②当0≤x＜0.5时，原方程可化为：x﹣2x+1＝5，解之，得x＝﹣4，

    经检验x不合题意，舍去．

    ③当x＜0时，原方程可化为：﹣x﹣2x+1＝5，它的解是x＝﹣．

    所以原方程的解是x＝2或x＝﹣．

    （1）根据上面的解题过程，写出方程2|x﹣1|﹣x＝4的解．

    （2）根据上面的解题过程，解方程：2|x﹣1|﹣|x|＝4．

    （3）方程|x|﹣2|x﹣1|＝4是否有解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程mx2﹣（2m﹣3）x+（m﹣1）=0有两个实数根．
    （1）求m的取值范围；
    （2）若m为正整数，求此方程的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：

    ①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°.其中结论正确的个数是（　　）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    同步练习册答案