
【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,C是劣弧 ![]() 的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2. 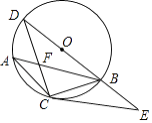
(1)求CB的长;
(2)延长DB到E,使BE=OB,连接CE,求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
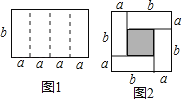
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=5,xy=4,求x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
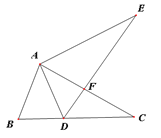
【题目】如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,∠BAD=∠CAE,AC=AE.
(1)求证:△ABC≌△ADE;
(2)若∠B=60°,求证:△ABD是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com