
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
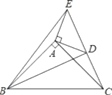
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
如图:
①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
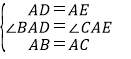 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ABD+∠DBC=45°.
∴∠ACE+∠DBC=45°,
∴②正确;
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠CAB=90°,
∴∠ABD+∠AFB=90°,
∴∠ACE+∠AFB=90°.
∵∠DFC=∠AFB,
∴∠ACE+∠DFC=90°,
∴∠FDC=90°.
∴BD⊥CE,
∴③正确;
④∵∠BAC=∠DAE=90°,∠BAC+∠DAE+∠BAE+∠DAC=360°,
∴∠BAE+∠DAC=180°,故④正确.
所以①②③④都正确,共计4个.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中,将点
在平面直角坐标系中,将点![]() 向右平移
向右平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() .直接写出点
.直接写出点![]() ,
,![]() 的坐标;23.
的坐标;23.
![]() 在平面直角坐标系中,将第二象限内的点
在平面直角坐标系中,将第二象限内的点![]() 向右平移
向右平移![]() 个单位到第一象限点
个单位到第一象限点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
![]() 在平面直角坐标系中.将点
在平面直角坐标系中.将点![]() 沿水平方向平移
沿水平方向平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF为平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
(3)在(2)的条件下,当AE=3时,求四边形BEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
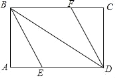
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
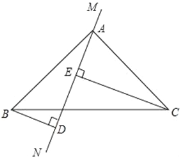
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,过点B作BD⊥MN于D,过C作CE⊥MN于E.
(1)求证:△ABD≌△CAE;
(2)若BD=12cm,DE=20cm,求CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
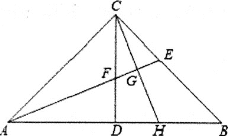
(1)直接写出∠CFE的度数________;
(2)求证:CF=BH.
查看答案和解析>>
科目:初中数学 来源: 题型:
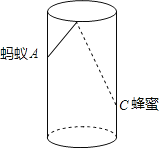
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com