
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
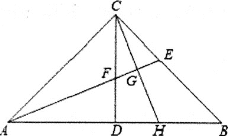
(1)直接写出∠CFE的度数________;
(2)求证:CF=BH.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( ) 
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
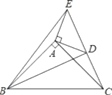
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1: ![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°.
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°. 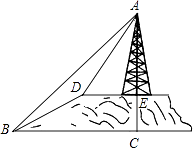
(1)求小山的高度;
(2)求铁架的高度.( ![]() ≈1.73,精确到0.1米)
≈1.73,精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图,若BC=BD,求证:CD=DE;
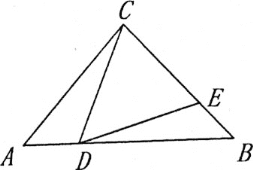
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,![]() ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.
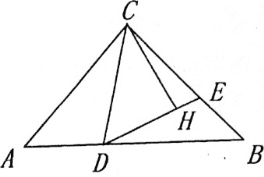
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴x=﹣1,下列五个代数式ab、ac、a﹣b+c、b2﹣4ac、2a+b中,值大于0的个数为( ) 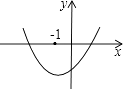
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2). 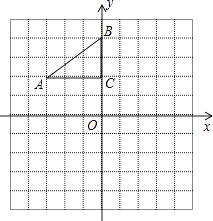
(1)①将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
②若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(2)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系. 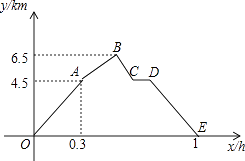
(1)小明骑车在平路上的速度为km/h;他途中休息了h;
(2)求线段AB、BC所表示的y与x之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com