
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABCЕФШ§ИіЖЅЕуЗжБ№ЪЧAЃЈЉ3ЃЌ2ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ 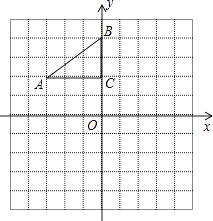
ЃЈ1ЃЉЂйНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁїA1B1CЃЛЦНвЦЁїABCЃЌШєЕуAЕФЖдгІЕуA2ЕФзјБъЮЊЃЈ0ЃЌЉ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁїA2B2C2ЃЛ
ЂкШєНЋЁїA1B1CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁїA2B2C2ЃЛЧыжБНгаДГіа§зЊжааФЕФзјБъЃЛ
ЃЈ2ЃЉдкxжсЩЯгавЛЕуPЃЌЪЙЕУPA+PBЕФжЕзюаЁЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЂйЁїABCа§зЊКѓЖдгІЕФЁїA1B1CЃЌЁїABCЦНвЦКѓЖдгІЕФЁїA2B2C2ШчЭМЫљЪО
ЂкШчЭМЫљЪОЃКа§зЊжааФЕФзјБъЮЊЃКЃЈ ![]() ЃЌЉ1ЃЉ
ЃЌЉ1ЃЉ
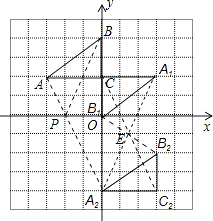
ЃЈ2ЃЉНтЃКЁпPOЁЮACЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
ЁрOP=2ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉ
ЁОНтЮіЁПЃЈ1ЃЉбгГЄACЕНA1 ЃЌ ЪЙЕУAC=A1CЃЌбгГЄBCЕНB1 ЃЌ ЪЙЕУBC=B1CЃЌРћгУЕуAЕФЖдгІЕуA2ЕФзјБъЮЊЃЈ0ЃЌЉ4ЃЉЃЌЕУГіЭМЯѓЦНвЦЕЅЮЛЃЌМДПЩЕУГіЁїA2B2C2ЃЛИљОнЁїЁїA1B1CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁїA2B2C2НјЖјЕУГіЃЌа§зЊжааФМДПЩЃЛЃЈ2ЃЉИљОнBЕуЙигкxжсЖдГЦЕуЮЊA2 ЃЌ СЌНгAA2 ЃЌ НЛxжсгкЕуPЃЌдйРћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓГіPЕузјБъМДПЩЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтжсЖдГЦ-зюЖЬТЗЯпЮЪЬтЕФЯрЙижЊЪЖЃЌеЦЮевбжЊЦ№ЕуНсЕуЃЌЧѓзюЖЬТЗОЖЃЛгыШЗЖЈЦ№ЕуЯрЗДЃЌвбжЊжеЕуНсЕуЃЌЧѓзюЖЬТЗОЖЃЛвбжЊЦ№ЕуКЭжеЕуЃЌЧѓСННсЕужЎМфЕФзюЖЬТЗОЖЃЛЧѓЭМжаЫљгазюЖЬТЗОЖЃЎ


 аЁбЇПЮЪБзївЕШЋЭЈСЗАИЯЕСаД№АИ
аЁбЇПЮЪБзївЕШЋЭЈСЗАИЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() дкЦНУцжБНЧзјБъЯЕжаЃЌНЋЕу
дкЦНУцжБНЧзјБъЯЕжаЃЌНЋЕу![]() ЯђгвЦНвЦ
ЯђгвЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌдйНЋЕу
ЃЌдйНЋЕу![]() ШЦзјБъдЕуЫГЪБеыа§зЊ
ШЦзјБъдЕуЫГЪБеыа§зЊ![]() ЕНЕу
ЕНЕу![]() ЃЎжБНгаДГіЕу
ЃЎжБНгаДГіЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЛ23.
ЕФзјБъЃЛ23.
![]() дкЦНУцжБНЧзјБъЯЕжаЃЌНЋЕкЖўЯѓЯоФкЕФЕу
дкЦНУцжБНЧзјБъЯЕжаЃЌНЋЕкЖўЯѓЯоФкЕФЕу![]() ЯђгвЦНвЦ
ЯђгвЦНвЦ![]() ИіЕЅЮЛЕНЕквЛЯѓЯоЕу
ИіЕЅЮЛЕНЕквЛЯѓЯоЕу![]() ЃЌдйНЋЕу
ЃЌдйНЋЕу![]() ШЦзјБъдЕуЫГЪБеыа§зЊ
ШЦзјБъдЕуЫГЪБеыа§зЊ![]() ЕНЕу
ЕНЕу![]() ЃЌжБНгаДГіЕу
ЃЌжБНгаДГіЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
![]() дкЦНУцжБНЧзјБъЯЕжаЃЎНЋЕу
дкЦНУцжБНЧзјБъЯЕжаЃЎНЋЕу![]() биЫЎЦНЗНЯђЦНвЦ
биЫЎЦНЗНЯђЦНвЦ![]() ИіЕЅЮЛЕНЕу
ИіЕЅЮЛЕНЕу![]() ЃЌдйНЋЕу
ЃЌдйНЋЕу![]() ШЦзјБъдЕуЫГЪБеыа§зЊ
ШЦзјБъдЕуЫГЪБеыа§зЊ![]() ЕНЕу
ЕНЕу![]() ЃЌжБНгаДГіЕу
ЃЌжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌЁїABCЕФИпCDгыНЧЦНЗжЯпAEЯрНЛЕуFЃЌЙ§ЕуCзїCHЁЭAEгкGЃЌНЛABгкHЃЎ
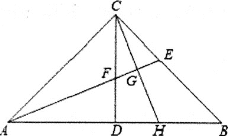
ЃЈ1ЃЉжБНгаДГіЁЯCFEЕФЖШЪ§________ЃЛ
ЃЈ2ЃЉЧѓжЄЃКCFЃНBHЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌDЮЊЁїABCФквЛЕуЃЌCDЦНЗжЁЯACBЃЌBDЁЭCDЃЌЁЯA=ЁЯABDЃЌШєAC=5ЃЌBC=3ЃЌдђBDЕФГЄЮЊЃЈЁЁЁЁЃЉ
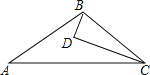
A. 1 B. 1.5 C. 2.5 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬЃК
ЂйЃЈ2x+1ЃЉ2=3ЃЈ2x+1ЃЉ
Ђк4ЃЈxЉ1ЃЉ2Љ9ЃЈ3Љ2xЃЉ2=0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
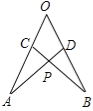
ЁОЬтФПЁПШчЭМЃКдкЁЯAOBЕФСНБпНиШЁOA=OBЃЌOC=ODЃЌСЌНгADЃЌBCНЛгкЕуPЃЌдђЯТСаНсТлжаЂйЁїAODЁеЁїBOCЃЌЂкЁїAPCЁеЁїBPDЃЌЂлЕуPдкЁЯAOBЕФЦНЗжЯпЩЯЁЃ е§ШЗЕФЪЧ ЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
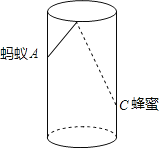
ЁОЬтФПЁПШчЭМЃЌдВжљаЮВЃСЇБИпЮЊ12cmЁЂЕзУцжмГЄЮЊ18cmЃЌдкБФкРыБЕз4cmЕФЕуC
ДІгавЛЕЮЗфУлЃЌДЫЪБвЛжЛТьвЯе§КУдкБЭтБкЃЌРыБЩЯби4cmгыЗфУлЯрЖдЕФЕуAДІЃЌдђТьвЯЕНДяЗфУлЕФзю
ЖЬОрРыЮЊ Ёј cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
ЪдЧѓЃКЃЈ1ЃЉ![]() ЕФЖШЪ§ЃЛЃЈ2ЃЉЫФБпаЮ
ЕФЖШЪ§ЃЛЃЈ2ЃЉЫФБпаЮ![]() ЕФУцЛ§ЃЈНсЙћБЃСєИљКХЃЉЃЛ
ЕФУцЛ§ЃЈНсЙћБЃСєИљКХЃЉЃЛ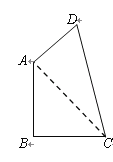
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫПМВьБљДЈЕФШкЛЏзДПіЃЌвЛжЇПЦПМЖгдкФГБљДЈЩЯЩшЖЈвЛИівдДѓБОгЊOЮЊдВаФЃЌАыОЖЮЊ4kmЕФдВаЮПМВьЧјгђЃЌЯпЖЮP1P2ЪЧБљДЈЕФВПЗжБпНчЯпЃЈВЛПМТЧЦфЫќБпНчЃЉЃЌЕББљДЈШкЛЏЪБЃЌБпНчЯпбизХгыЦфДЙжБЕФЗНЯђГЏПМВьЧјгђЦНаавЦЖЏЃЌШєОЙ§nФъЃЌБљДЈЕФБпНчЯпP1P2вЦЖЏЕФОрРыЮЊsЃЈkmЃЉЃЌВЂЧвsгыnЃЈnЮЊе§ећЪ§ЃЉЕФЙиЯЕЪЧs= ![]() n2Љ
n2Љ ![]() n+
n+ ![]() ЃЎвдOЮЊдЕуЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЦфжаP1ЁЂP2ЕФзјБъЗжБ№ЮЊЃЈЉ4ЃЌ9ЃЉЁЂЃЈЉ13ЁЂЉ3ЃЉЃЎ
ЃЎвдOЮЊдЕуЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЦфжаP1ЁЂP2ЕФзјБъЗжБ№ЮЊЃЈЉ4ЃЌ9ЃЉЁЂЃЈЉ13ЁЂЉ3ЃЉЃЎ 
ЃЈ1ЃЉЧѓЯпЖЮP1P2ЫљдкжБЯпЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓБљДЈБпНчЯпвЦЖЏЕНПМВьЧјгђЫљашЕФзюЖЬЪБМфЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com