
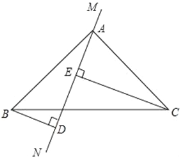
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,过点B作BD⊥MN于D,过C作CE⊥MN于E.
(1)求证:△ABD≌△CAE;
(2)若BD=12cm,DE=20cm,求CE的长度.
【答案】(1)见解析;(2)32.
【解析】
(1)由∠BAC=90°,则∠BAD+∠CAD=90°,又BD⊥MN,CE⊥MN,则∠CAD+∠ACE=90°,∠BDA=∠AEC=90°,AAS即可证明△ABD≌△CAE;
(2)由(1)得,BD=AE,AD=CE,由BD=12cm,则AE=12cm,又DE=20cm,则AD=AE+DE=12cm+20cm=32cm,所以,CE=AD=32cm;
(1)证明:∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
又∵BD⊥MN,CE⊥MN,
∴∠CAD+∠ACE=90°,∠BDA=∠AEC=90°,
∴∠BAD=∠ACE,又AB=AC,
在△ABD和△CAE中
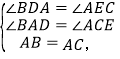 ,
,
∴△ABD≌△CAE(AAS);
(2)解:∵△ABD≌△CAE,
∴BD=AE,AD=CE,
∵BD=12cm,DE=20cm,
∴AE=12cm,AD=AE+DE=12cm+20cm=32cm,
∴CE=32cm.


科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D交AC于点E,那么下列结论中正确的是 ( )
①△BDF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF=CF

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k> ![]()
B.k≥ ![]()
C.k> ![]() 且k≠1
且k≠1
D.k≥ ![]() 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
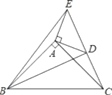
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,BC∥x轴,点A,C在反比例函数y= ![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y= ![]() (x>0)的图象上,则△ABC的面积为 .
(x>0)的图象上,则△ABC的面积为 . 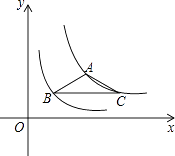
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1: ![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°.
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°. 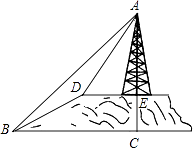
(1)求小山的高度;
(2)求铁架的高度.( ![]() ≈1.73,精确到0.1米)
≈1.73,精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴x=﹣1,下列五个代数式ab、ac、a﹣b+c、b2﹣4ac、2a+b中,值大于0的个数为( ) 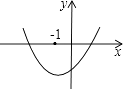
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 已知a,b,c是三角形的三边,则a2+b2=c2
B. 在直角三角形中,两边的平方和等于第三边的平方
C. 在Rt△ABC中,∠![]() ,所以a2+b2=c2
,所以a2+b2=c2
D. 在Rt△ABC中,∠![]() ,所以a2+b2=c2
,所以a2+b2=c2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com