
ЁОЬтФПЁПШчЭМЃЌЙ§дЕуЕФжБЯпy=k1xКЭy=k2xгыЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓЗжБ№НЛгкСНЕуAЃЌCКЭBЃЌDЃЌСЌНгABЃЌBCЃЌCDЃЌDAЃЎ
ЕФЭМЯѓЗжБ№НЛгкСНЕуAЃЌCКЭBЃЌDЃЌСЌНгABЃЌBCЃЌCDЃЌDAЃЎ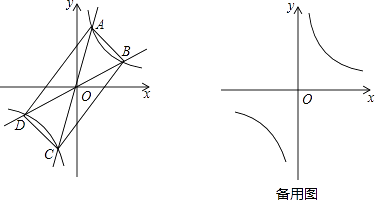
ЃЈ1ЃЉЫФБпаЮABCDвЛЖЈЪЧЫФБпаЮЃЛЃЈжБНгЬюаДНсЙћЃЉ
ЃЈ2ЃЉЫФБпаЮABCDПЩФмЪЧОиаЮТ№ЃПШєПЩФмЃЌЪдЧѓДЫЪБk1 ЃЌ k2жЎМфЕФЙиЯЕЪНЃЛШєВЛФмЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшPЃЈx1 ЃЌ y1ЃЉЃЌQЃЈx2 ЃЌ y2ЃЉЃЈx2ЃОx1ЃО0ЃЉЪЧКЏЪ§y= ![]() ЭМЯѓЩЯЕФШЮвтСНЕуЃЌa=
ЭМЯѓЩЯЕФШЮвтСНЕуЃЌa= ![]() ЃЌb=
ЃЌb= ![]() ЃЌЪдХаЖЯaЃЌbЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЌЪдХаЖЯaЃЌbЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉЦНаа
ЃЈ2ЃЉ
НтЃКЁпе§БШР§КЏЪ§y=k1xЃЈk1ЃО0ЃЉгыЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓдкЕквЛЯѓЯоЯрНЛгкAЃЌ
ЕФЭМЯѓдкЕквЛЯѓЯоЯрНЛгкAЃЌ
Ёрk1x= ![]() ЃЌНтЕУx=
ЃЌНтЕУx= ![]() ЃЈвђЮЊНЛгкЕквЛЯѓЯоЃЌЫљвдИКИљЩсШЅЃЌжЛБЃСєе§ИљЃЉ
ЃЈвђЮЊНЛгкЕквЛЯѓЯоЃЌЫљвдИКИљЩсШЅЃЌжЛБЃСєе§ИљЃЉ
НЋx= ![]() ДјШыy=k1xЕУy=
ДјШыy=k1xЕУy= ![]() ЃЌ
ЃЌ
ЙЪAЕуЕФзјБъЮЊЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЭЌРэдђBЕузјБъЮЊЃЈ
ЃЉЭЌРэдђBЕузјБъЮЊЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
гжЁпOA=OBЃЌ
Ёр ![]() =
= ![]() ЃЌСНБпЦНЗНЕУЃК
ЃЌСНБпЦНЗНЕУЃК ![]() +k1=
+k1= ![]() +k2ЃЌ
+k2ЃЌ
ећРэКѓЕУЃЈk1Љk2ЃЉЃЈk1k2Љ1ЃЉ=0ЃЌ
Ёпk1Ёйk2ЃЌ
Ыљвдk1k2Љ1=0ЃЌМДk1k2=1ЃЛ
ЃЈ3ЃЉ
НтЃКЁпPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉЃЈx2ЃОx1ЃО0ЃЉЪЧКЏЪ§y= ![]() ЭМЯѓЩЯЕФШЮвтСНЕуЃЌ
ЭМЯѓЩЯЕФШЮвтСНЕуЃЌ
Ёрy1= ![]() ЃЌy2=
ЃЌy2= ![]() ЃЌ
ЃЌ
Ёрa= ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрaЉb= ![]() Љ
Љ ![]() =
= ![]() =
= ![]() ЃЌ
ЃЌ
Ёпx2ЃОx1ЃО0ЃЌ
Ёр ![]() ЃО0ЃЌx1x2ЃО0ЃЌЃЈx1+x2ЃЉЃО0ЃЌ
ЃО0ЃЌx1x2ЃО0ЃЌЃЈx1+x2ЃЉЃО0ЃЌ
Ёр ![]() ЃО0ЃЌ
ЃО0ЃЌ
ЁрaЉbЃО0ЃЌ
ЁрaЃОbЃЎ
ЁОНтЮіЁПНтЃКЃЈ1ЃЉЁпжБЯпy=k1xКЭy=k2xгыЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓЙигкдЕуЖдГЦЃЌ
ЕФЭМЯѓЙигкдЕуЖдГЦЃЌ
ЁрOA=OCЃЌOB=ODЃЌ
ЁрЫФБпаЮABCD ЪЧЦНааЫФБпаЮЃЛ
ЫљвдД№АИЪЧЃКЦНааЃЛ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љ ![]() x2+bx+eгыxжсНЛгкЕуAЃЈЉ3ЃЌ0ЃЉЁЂЕуBЃЈ9ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌЖЅЕуЮЊDЃЌСЌНгADЁЂDBЃЌЕуPЮЊЯпЖЮADЩЯвЛЖЏЕуЃЎ
x2+bx+eгыxжсНЛгкЕуAЃЈЉ3ЃЌ0ЃЉЁЂЕуBЃЈ9ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌЖЅЕуЮЊDЃЌСЌНгADЁЂDBЃЌЕуPЮЊЯпЖЮADЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуPзїBDЕФЦНааЯпЃЌНЛABгкЕуQЃЌСЌНгDQЃЌЩшAQ=mЃЌЁїPDQЕФУцЛ§ЮЊSЃЌЧѓSЙигкmЕФКЏЪ§НтЮіЪНЃЌвдМАSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌХзЮяЯпЖдГЦжсгыxжсНЛгыЕуGЃЌEЮЊOGЕФжаЕуЃЌFЮЊЕуCЙигкDGЖдГЦЕФЖдГЦЕуЃЌЙ§ЕуPЗжБ№зїжБЯпEFЁЂDGЕФДЙЯпЃЌДЙзуЮЊMЁЂNЃЌСЌНгMNЃЌжБНгаДГіЁїPMNЮЊЕШбќШ§НЧаЮЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯгаЕуaЃЌbЃЌcШ§Еу
![]()
ЃЈ1ЃЉгУЁАЃМЁБНЋaЃЌbЃЌcСЌНгЦ№РДЃЎ
ЃЈ2ЃЉbЉaЁЁ ЁЁ1ЃЈЬюЁАЃМЁБЁАЃОЁБЃЌЁАЃНЁБЃЉ
ЃЈ3ЃЉЛЏМђ|cЉb|Љ|cЉa+1|+|aЉ1|
ЃЈ4ЃЉгУКЌaЃЌbЕФЪНзгБэЪОЯТСаЕФзюаЁжЕЃК
Ђй|xЉa|+|xЉb|ЕФзюаЁжЕЮЊЁЁ ЁЁЃЛ
Ђк|xЉa|+|xЉb|+|x+1|ЕФзюаЁжЕЮЊЁЁ ЁЁЃЛ
Ђл|xЉa|+|xЉb|+|xЉc|ЕФзюаЁжЕЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯA=30ЁуЃЌAB=4ЃЎ 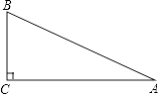
ЃЈ1ЃЉзїACБпЩЯЕФДЙжБЦНЗжЯпDEЃЌНЛACгкЕуDЃЌНЛABгкЕуEЃЈгУГпЙцзїЭМЗЈЃЌБЃСєзїЭМКлМЃЃЌВЛвЊЧѓаДзїЗЈКЭжЄУїЃЉЃК
ЃЈ2ЃЉСЌНгCEЃЌЧѓЁїBECЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФЯвЃЌCЪЧСгЛЁ ![]() ЕФжаЕуЃЌСЌBOВЂбгГЄНЛЁбOгкЕуDЃЌСЌНгCAЃЌCBЃЌABгыCDНЛгкЕуFЃЌвбжЊCF=1ЃЌFD=2ЃЎ
ЕФжаЕуЃЌСЌBOВЂбгГЄНЛЁбOгкЕуDЃЌСЌНгCAЃЌCBЃЌABгыCDНЛгкЕуFЃЌвбжЊCF=1ЃЌFD=2ЃЎ 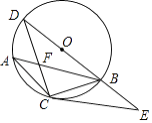
ЃЈ1ЃЉЧѓCBЕФГЄЃЛ
ЃЈ2ЃЉбгГЄDBЕНEЃЌЪЙBE=OBЃЌСЌНгCEЃЌЧѓжЄЃКCEЪЧЁбOЕФЧаЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуNЪЧЗДБШР§КЏЪ§y= ![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуNзїMNЁЮxжсЃЌНЛжБЯпy=Љ2x+4гкЕуMЃЌдђЁїOMNУцЛ§ЕФзюаЁжЕЪЧЃЈ ЃЉ
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуNзїMNЁЮxжсЃЌНЛжБЯпy=Љ2x+4гкЕуMЃЌдђЁїOMNУцЛ§ЕФзюаЁжЕЪЧЃЈ ЃЉ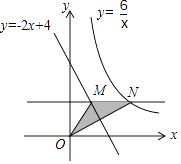
A.1
B.2
C.3
D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДгЦТЩЯНЈжўЮяABЙлВтЦТЕзНЈжўЮяCDЃЎДгAЕуВтЕУCЕуЕФИЉНЧЮЊ45ЁуЃЌДгBЕуВтЕУDЕуЕФИЉНЧЮЊ30ЁуЃЎвбжЊABЕФИпЖШЮЊ10mЃЌABгыCDЕФЫЎЦНОрРыЪЧOD=15mЃЌдђCDЕФИпЖШЮЊmЃЈНсЙћБЃСєИљКХЃЉ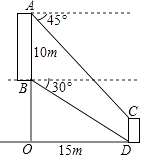
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
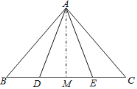
ЁОЬтФПЁПвбжЊЕу![]() ЁЂ
ЁЂ![]() дк
дк![]() ЕФ
ЕФ![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЮЊСЫХаЖЯ
ЃЌЮЊСЫХаЖЯ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЃЌЧыФуЬюПеЭъГЩЯТУцЕФЭЦРэЙ§ГЬЃЌВЂдкПеАзРЈКХФкЃЌзЂУїЭЦРэЕФИљОнЃЎ
ЕФДѓаЁЙиЯЕЃЌЧыФуЬюПеЭъГЩЯТУцЕФЭЦРэЙ§ГЬЃЌВЂдкПеАзРЈКХФкЃЌзЂУїЭЦРэЕФИљОнЃЎ
НтЃКзї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]()
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЪЧ________Ш§НЧаЮЃЌ
ЪЧ________Ш§НЧаЮЃЌ
Ёр![]() ________
________
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ________ЃЌМД
________ЃЌМД![]() ________ЃЛ
________ЃЛ
гжЁп________ЃЈздМКЫљзїЃЉЃЌ
Ёр![]() ЪЧЯпЖЮ________ЕФДЙжБЦНЗжЯпЃЛ
ЪЧЯпЖЮ________ЕФДЙжБЦНЗжЯпЃЛ
Ёр![]() ________
________
Ёр________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
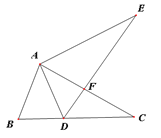
ЁОЬтФПЁПШчЭМЃЌЕуEдкЁїABCЭтВПЃЌЕуDдкBCБпЩЯЃЌDEНЛACгкЕуFЃЌШєЁЯC=ЁЯEЃЌЁЯBAD=ЁЯCAEЃЌAC=AEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABCЁеЁїADEЃЛ
ЃЈ2ЃЉШєЁЯB=60ЁуЃЌЧѓжЄЃКЁїABDЪЧЕШБпШ§НЧаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com