
ЁОЬтФПЁПдФЖСЯТСаР§Ьт
НтЗНГЬЃК|x|+|2xЉ1|ЃН5ЃЎ
НтЃКЂйЕБxЁн0.5ЪБЃЌдЗНГЬПЩЛЏЮЊЃКx+2xЉ1ЃН5ЃЌЫќЕФНтЪЧxЃН2ЃЛ
ЂкЕБ0ЁмxЃМ0.5ЪБЃЌдЗНГЬПЩЛЏЮЊЃКxЉ2x+1ЃН5ЃЌНтжЎЃЌЕУxЃНЉ4ЃЌ
ОМьбщxВЛКЯЬтвтЃЌЩсШЅЃЎ
ЂлЕБxЃМ0ЪБЃЌдЗНГЬПЩЛЏЮЊЃКЉxЉ2x+1ЃН5ЃЌЫќЕФНтЪЧxЃНЉ![]() ЃЎ
ЃЎ
ЫљвддЗНГЬЕФНтЪЧxЃН2ЛђxЃНЉ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉИљОнЩЯУцЕФНтЬтЙ§ГЬЃЌаДГіЗНГЬ2|xЉ1|ЉxЃН4ЕФНтЃЎ
ЃЈ2ЃЉИљОнЩЯУцЕФНтЬтЙ§ГЬЃЌНтЗНГЬЃК2|xЉ1|Љ|x|ЃН4ЃЎ
ЃЈ3ЃЉЗНГЬ|x|Љ2|xЉ1|ЃН4ЪЧЗёгаНтЃЎ
ЁОД№АИЁПЃЈ1ЃЉдЗНГЬЕФНтЪЧxЃН6ЛђxЃНЉ![]() ЃЛЃЈ2ЃЉдЗНГЬЕФНтЪЧxЃН6ЛђxЃН-2ЃЛЃЈ3ЃЉдЗНГЬЮоНтЃЎ
ЃЛЃЈ2ЃЉдЗНГЬЕФНтЪЧxЃН6ЛђxЃН-2ЃЛЃЈ3ЃЉдЗНГЬЮоНтЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЗжxЁн1КЭxЃМ1НтГіЗНГЬЃЛ
ЃЈ2ЃЉЗжxЁн1ЃЌ0ЃМxЃМ1ЃЌxЃМ0НтГіЗНГЬЃЛ
ЃЈ3ЃЉНсКЯЃЈ2ЃЉЕФЗНЗЈКЭНсТлЃЌевГіД№АИЃЎ
ЃЈ1ЃЉ2|xЉ1|ЉxЃН4
ЂйЕБxЁн1ЪБЃЌдЗНГЬПЩЛЏЮЊЃК2xЉ2ЉxЃН4ЃЌЫќЕФНтЪЧxЃН6ЃЛ
ЂкЕБxЃМ1ЪБЃЌдЗНГЬПЩЛЏЮЊЃК2Љ2xЉxЃН4ЃЌНтЕУxЃНЉ![]() ЃЛ
ЃЛ
ЫљвддЗНГЬЕФНтЪЧxЃН6ЛђxЃНЉ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉ2|xЉ1|Љ|x|ЃН4ЃЎ
ЂйЕБxЁн1ЪБЃЌдЗНГЬПЩЛЏЮЊЃК2xЉ2ЉxЃН4ЃЌЫќЕФНтЪЧxЃН6ЃЛ
ЂкЕБ0ЁмxЃМ1ЪБЃЌдЗНГЬПЩЛЏЮЊЃК2Љ2xЉxЃН4ЃЌНтЕУxЃНЉ![]() ЃЌ
ЃЌ
ОМьбщxВЛКЯЬтвтЃЌЩсШЅЃЎ
ЂлЕБxЃМ0ЪБЃЌдЗНГЬПЩЛЏЮЊЃК2Љ2x+xЃН4ЃЌЫќЕФНтЪЧxЃН-2ЃЎ
ЫљвддЗНГЬЕФНтЪЧxЃН6ЛђxЃН-2ЃЎ
ЃЈ3ЃЉ|x|Љ2|xЉ1|ЃН4
ЂйЕБxЁн1ЪБЃЌдЗНГЬПЩЛЏЮЊЃКxЉ2x+2ЃН4ЃЌЫќЕФНтЪЧxЃНЉ2ЃЛ
ОМьбщxВЛКЯЬтвтЃЌЩсШЅЃЎ
ЂкЕБ0ЁмxЃМ1ЪБЃЌдЗНГЬПЩЛЏЮЊЃКxЉ2+2xЃН4ЃЌНтЕУxЃН2ЃЌ
ОМьбщxВЛКЯЬтвтЃЌЩсШЅЃЎ
ЂлЕБxЃМ0ЪБЃЌдЗНГЬПЩЛЏЮЊЃКЉxЉ2+2xЃН4ЃЌЫќЕФНтЪЧxЃН6ЃЎ
ОМьбщxВЛКЯЬтвтЃЌЩсШЅЃЎ
ЫљвддЗНГЬЮоНтЃЎ


 гРЧЌНЬг§КЎМйзївЕПьРжМйЦкбгБпШЫУёГіАцЩчЯЕСаД№АИ
гРЧЌНЬг§КЎМйзївЕПьРжМйЦкбгБпШЫУёГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДгЦТЩЯНЈжўЮяABЙлВтЦТЕзНЈжўЮяCDЃЎДгAЕуВтЕУCЕуЕФИЉНЧЮЊ45ЁуЃЌДгBЕуВтЕУDЕуЕФИЉНЧЮЊ30ЁуЃЎвбжЊABЕФИпЖШЮЊ10mЃЌABгыCDЕФЫЎЦНОрРыЪЧOD=15mЃЌдђCDЕФИпЖШЮЊmЃЈНсЙћБЃСєИљКХЃЉ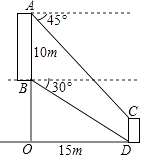
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
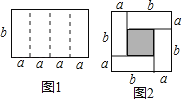
ЁОЬтФПЁПШчЭМ1ЪЧвЛИіГЄЮЊ4aЁЂПэЮЊbЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖЦНОљЗжГЩЫФПщаЁГЄЗНаЮЃЌШЛКѓгУЫФПщаЁГЄЗНаЮЦДГЩЕФвЛИіЁАЛиаЮЁБе§ЗНаЮЃЈШчЭМ2ЃЉЃЎ
ЃЈ1ЃЉЭМ2жавѕгАВПЗжЕФУцЛ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЙлВьЭМ2ЃЌЧыФуаДГіЃЈa+bЃЉ2ЁЂЃЈaЉbЃЉ2ЁЂabжЎМфЕФЕШСПЙиЯЕЪЧЁЁ ЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЕФНсТлЃЌШєx+y=5ЃЌxy=4ЃЌЧѓxЉyЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
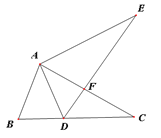
ЁОЬтФПЁПШчЭМЃЌЕуEдкЁїABCЭтВПЃЌЕуDдкBCБпЩЯЃЌDEНЛACгкЕуFЃЌШєЁЯC=ЁЯEЃЌЁЯBAD=ЁЯCAEЃЌAC=AEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABCЁеЁїADEЃЛ
ЃЈ2ЃЉШєЁЯB=60ЁуЃЌЧѓжЄЃКЁїABDЪЧЕШБпШ§НЧаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШБпШ§НЧаЮABCЕФЭтВрзїжБЯпAPЃЌЕуCЙигкжБЯпAPЕФЖдГЦЕуЮЊЕуDЃЌСЌНгADЃЌBDЃЌЦфжаBDНЛжБЯпAPгкЕуE.
ЃЈ1ЃЉвРЬтвтВЙШЋЭМаЮЃЛЃЈ2ЃЉШєЁЯPACЃН20ЁуЃЌЧѓЁЯAEBЕФЖШЪ§ЃЛ
ЃЈ3ЃЉСЌНсCEЃЌаДГіAE, BE, CEжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌCDгыCEЗжБ№ЪЧаББпABЩЯЕФИпгыжаЯпЃЌвдЯТХаЖЯжае§ШЗЕФИіЪ§гаЃЈЁЁЁЁЃЉ
ЂйЁЯDCB=ЁЯAЃЛЂкЁЯDCB=ЁЯACEЃЛЂлЁЯACD=ЁЯBCEЃЛЂмЁЯBCE=ЁЯBECЃЎ
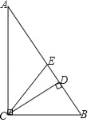
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЁЂAЁфDЁфЗжБ№ЪЧШёНЧЁїABCКЭЁїAЁфBЁфCЁфжаBCгыBЁфCЁфБпЩЯЕФИпЃЌЧвAB=AЁфBЁфЃЌAD=AЁфDЁфЃЌШєЪЙЁїABCЁеЁїAЁфBЁфCЁфЃЌЧыФуВЙГфЬѕМў________ЃЎЃЈжЛашЬюаДвЛИіФуШЯЮЊЪЪЕБЕФЬѕМўЃЉ
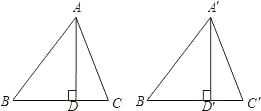
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com