
【题目】如图,AD、A′D′分别是锐角△ABC和△A′B′C′中BC与B′C′边上的高,且AB=A′B′,AD=A′D′,若使△ABC≌△A′B′C′,请你补充条件________.(只需填写一个你认为适当的条件)
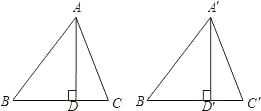
【答案】∠BAC=∠B'A'C'或∠C=∠C'或BC=B'C'
【解析】
已知AB=A′B′,A′D′=AD;根据斜边直角边定理即可证得Rt△ABD≌Rt△A'B'D',由此可得出∠B=∠B',因此△ABC和△A'B'C'中,已知AB=A'B',∠B=∠B',只需再添加一组对应角相等或BC=B'C'即可证得两三角形全等.
∵AB=A′B′,A′D′=AD,
∴Rt△ABD≌Rt△A'B'D'(HL);
∴∠B=∠B',
又∵AB=A'B',
∴当∠BAC=∠B'A'C'或∠C=∠C'或BC=B'C'时,△ABC≌△A'B'C'.
故答案为:∠BAC=∠B'A'C'或∠C=∠C'或BC=B'C'


科目:初中数学 来源: 题型:
【题目】阅读下列例题
解方程:|x|+|2x﹣1|=5.
解:①当x≥0.5时,原方程可化为:x+2x﹣1=5,它的解是x=2;
②当0≤x<0.5时,原方程可化为:x﹣2x+1=5,解之,得x=﹣4,
经检验x不合题意,舍去.
③当x<0时,原方程可化为:﹣x﹣2x+1=5,它的解是x=﹣![]() .
.
所以原方程的解是x=2或x=﹣![]() .
.
(1)根据上面的解题过程,写出方程2|x﹣1|﹣x=4的解.
(2)根据上面的解题过程,解方程:2|x﹣1|﹣|x|=4.
(3)方程|x|﹣2|x﹣1|=4是否有解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
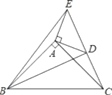
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).
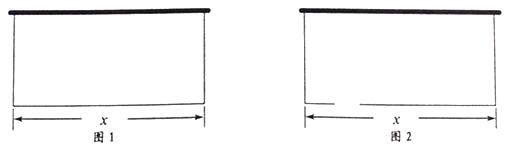
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,4)和B(﹣1,﹣5)两点.
(1)求出该一次函数的表达式;
(2)判断(﹣4,3)是否在这个函数的图象上?
(3)求出该函数图象与坐标轴的交点坐标以及与坐标轴围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
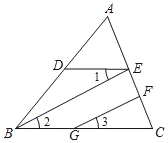
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式; 当4<x≤16时,写出一个符合表中数据的函数解析式;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min. 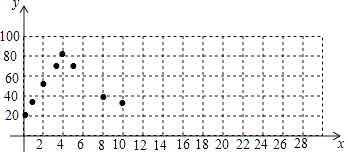
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com