
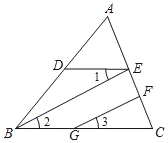
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
【答案】两直线平行同位角相等,已知,∠2,等量代换,BC,内错角相等两直线平行,两直线平行同旁内角互补,70
【解析】
利用平行线的性质和判定即可解决问题.
∵BE∥GF(已知),
∴∠2=∠3(两直线平行同位角相等),
∵∠1=∠3(已知),
∴∠1=∠2(等量代换),
∴DE∥BC(内错角相等两直线平行),
∴∠EDB+∠DBC=180°(两直线平行同旁内角互补),
∴∠EDB=180°﹣∠DBC(等式性质),
∵∠DBC=70°(已知),
∴∠EDB=180°﹣70°=110°.
故答案为:两直线平行同位角相等,已知,∠2,等量代换,BC,内错角相等两直线平行,两直线平行同旁内角互补,70.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
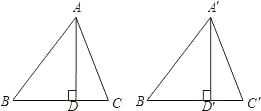
【题目】如图,AD、A′D′分别是锐角△ABC和△A′B′C′中BC与B′C′边上的高,且AB=A′B′,AD=A′D′,若使△ABC≌△A′B′C′,请你补充条件________.(只需填写一个你认为适当的条件)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.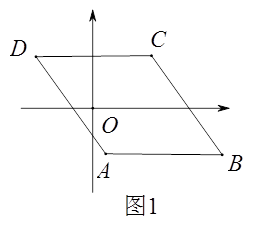

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以40元/千克的进价购进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售价x(元/千克)成一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)若该商店销售这批茶叶的成本不超过2800元,则它的最低销售价应定为多少元? 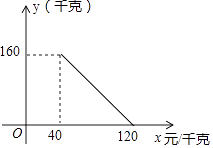
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
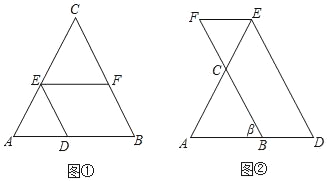
如图①,在△ABC中,点D、E、F分别在边AB、AC、CB上,且DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.请将下面的解答过程补充完整,并填空(理由或数学式):
解:∵DE∥BC( )
∴∠DEF= ( )
∵EF∥AB
∴ =∠ABC( )
∴∠DEF=∠ABC( )
∵∠ABC=65°
∴∠DEF=
应用:
如图②,在△ABC中,点D、E、F分别在边AB、AC、BC的延长线上,且DE∥BC,EF∥AB,若∠ABC=β,则∠DEF的大小为 (用含β的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为BC边的中点,BE平分∠ABC,交AD于E,F为△ABC外一点,且∠ACF=![]() ∠ACB,BE=CF,
∠ACB,BE=CF,
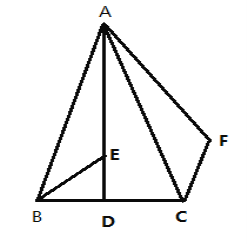
(1)求证:∠BAF=3∠BAD
(2)若DE=5,AE=13,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
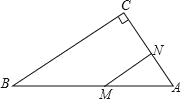
【题目】如图,在 Rt△ABC 中,∠C=90°,∠A=60°,AB=10cm,若点M 从点 B 出发以 2cm/s 的速度向点 A 运动,点 N 从点 A 出发以 1cm/s 的速度向点 C 运动,设 M、N 分别从点 B、A 同时出发,运动的时间为 ts.
(1)用含 t 的式子表示线段 AM、AN 的长;
(2)当 t 为何值时,△AMN 是以 MN 为底边的等腰三角形?
(3)当 t 为何值时,MN∥BC?并求出此时 CN 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com