
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.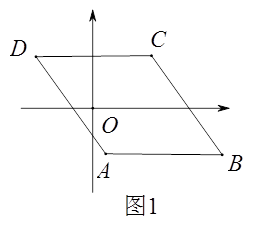

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
【答案】
(1)
解:在□ABCD中, CD=AB=6,
所以点P与点C重合,
所以点P的坐标为(3,4).
(2)
解:①当点P在边AD上时,
由已知得,直线AD的函数表达式为y=-2x-2,
设P(a,-2a-2),且-3≤a≤1,
若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,
所以2a+2=a-1,解得a=-3,此时P(-3,4)。
若点P关于y轴对称点Q2(-a,-2a-2)在直线y=x-1上,
所以-2a-2=-a-1,解得a=-1,此时P(-1,0).
②当点P在边AB上时,设P(a,-4),且1≤a≤7,
若点P关于x轴对称点Q3(a,4)在直线y=x-1上,
所以4=a-1,解得a=5,此时P(5,-4).
若点P关于y轴对称点Q4(-a,-4)在直线y=x-1上,
所以-4=-a-1,解得a=3,此时P(3,-4).
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)
解:因为直线AD为y=-2x-2,所以G(0,-2).
①如图,当点P在CD边上时,可设P(m,4),且-3≤m≤3,
则可得M′P=PM=4+2=6,M′G=GM=|m|,
易证得△OGM′~△HM′P,
则 ![]() ,
,
即 ![]() ,
,
则OM′= ![]() ,
,
在Rt△OGM′中,
由勾股定理得, ![]() ,
,
解得m= ![]() 或
或 ![]() ,
,
则P( ![]() ,4)或(
,4)或( ![]() ,4);
,4);

②如下图,当点P在AD边上时,设P(m,-2m-2),
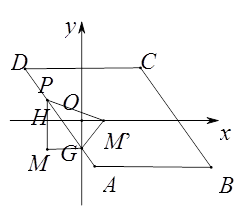
则PM′=PM=|-2m|,GM′=MG=|m|,
易证得△OGM′~△HM′P,
则 ![]() ,
,
即 ![]() ,
,
则OM′= ![]() ,
,
在Rt△OGM′中,
由勾股定理得, ![]() ,
,
整理得m= ![]() ,
,
则P( ![]() ,3);
,3);
如下图,当点P在AB边上时,设P(m,-4),
此时M′在y轴上,则四边形PM′GM是正方形,
所以GM=PM=4-2=2,
则P(2,-4).

综上所述,点P的坐标为(2,-4)或( ![]() ,3)或(
,3)或( ![]() ,4)或(
,4)或( ![]() ,4).
,4).
【解析】(1)点P在BC上,要使PD=CD,只有P与C重合;(2)首先要分点P在边AB,AD上时讨论,根据“点P关于坐标轴对称的点Q”,即还要细分“点P关于x轴的对称点Q和点P关于y轴的对称点Q”讨论,根据关于x轴、y轴对称点的特征(关于x轴对称时,点的横坐标不变,纵坐标变成相反数;关于y轴对称时,相反;)将得到的点Q的坐标代入直线y=x-1,即可解答;(3)在不同边上,根据图象,点M翻折后,点M’落在x轴还是y轴,可运用相似求解.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是( )

A. 150° B. 130° C. 140° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.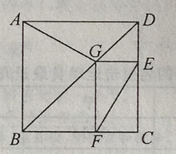
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).
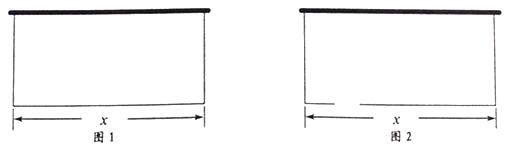
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.”
查看答案和解析>>
科目:初中数学 来源: 题型:
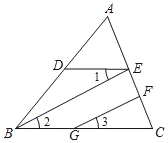
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD. 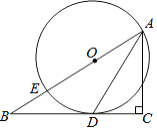
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC= ![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
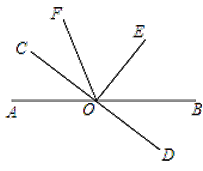
【题目】如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,
(1)求∠BOD的度数;
(2)写出图中所有与∠BOE互余的角,它们分别是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
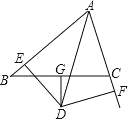
【题目】如图,G 为 BC 的中点,且 DG⊥BC,DE⊥AB 于 E,DF⊥AC 于 F, BE=CF.
(1)求证:AD 是∠BAC 的平分线;
(2)如果 AB=8,AC=6,求 AE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com