
【题目】如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是( )

A. 150° B. 130° C. 140° D. 120°
科目:初中数学 来源: 题型:
【题目】某公司计划从本地向甲、乙两地运送海产品进行销售.本地与甲、乙两地都有铁路和公路相连(如图所示),铁路的单位运价为2元/(吨千米),公路的单位运价为3元/(吨千米) 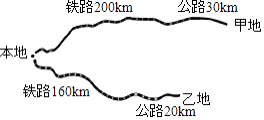
(1)若公司计划往甲、乙两地运输海产品共需铁路运费3680元,公路运费780元,求计划从本地向甲乙两地运输海产品各多少吨?
(2)经市场调查发现,甲地海产品的实际需求量比计划减少a(a>0)吨,但运到甲、乙两地的总量不变,且运到甲地的海产品不少于运到乙地的海产品,当a为多少时,实际总运费w最低?最低总运费是多少? (参考公式:货运运费=单位运价×运输里程×货物重量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= ![]() (m≠0)交于点A(2,﹣3)和点B(n,2).
(m≠0)交于点A(2,﹣3)和点B(n,2). 
(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= ![]() (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
(m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.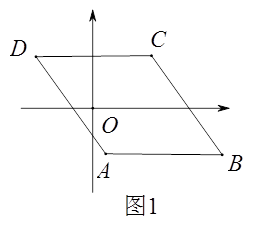

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com