
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= ![]() (m≠0)交于点A(2,﹣3)和点B(n,2).
(m≠0)交于点A(2,﹣3)和点B(n,2). 
(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= ![]() (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
(m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
科目:初中数学 来源: 题型:
【题目】观察下列等式 12=1= ![]() ×1×2×(2+1)
×1×2×(2+1)
12+22= ![]() ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ![]() ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ![]() ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一扇窗户,窗框为铝合金材料,下面是由两个大小相等的长方形窗框构成,上面是由三个大小相等的扇形组成的半圆窗框构成,窗户半圆部分安装彩色玻璃,两个长方形部分安装透明玻璃(本题中π取3,长度单位为米).
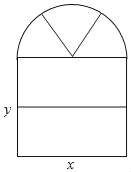
(1)一扇这样窗户一共需要铝合金多少米?(用含x,y的代数式表示)
(2)一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含x,y的代数式表示)
(3)某公司需要购进20扇窗户,在同等质量的前提下,甲、乙两个厂商分别给出如下报价:
铝合金(米/元) | 彩色玻璃(平方米/元) | 透明玻璃(平方米/元) | |
甲厂商 | 200 | 80 | 不超过100平方米的部分,90元/平方米,超过100平方米的部分,70元/平方米 |
乙厂商 | 220 | 60 | 80元/平方米,每购1平方米透明玻璃送0.1米铝合金 |
当x=2,y=3时,该公司在哪家厂商购买窗户合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是( )

A. 150° B. 130° C. 140° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
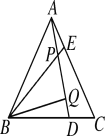
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.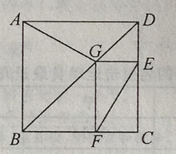
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD. 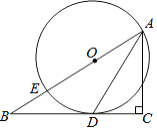
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC= ![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com