
ҰңМвДүҰүИзНәӘ¬Т»ЙИө°»§Ә¬ө°үтОҒВБғПҢрІДБПӘ¬ПВГжКЗУЙБҢёцөуРҰПаµИµДі¤·ҢРОө°үт№№іЙӘ¬ЙПГжКЗУЙИэёцөуРҰПаµИµДЙИРОЧйіЙµД°лФІө°үт№№іЙӘ¬ө°»§°лФІІү·Ц°ІЧ°ІКЙ«ІӘБ§Ә¬БҢёці¤·ҢРОІү·Ц°ІЧ°НёГчІӘБ§(±ңМвЦР¦РИҰ3Ә¬і¤¶ИµӨО»ОҒГЧ)Ә®
(1)Т»ЙИХвСщө°»§Т»№ІРиТҒВБғПҢр¶аЙЩГЧӘү(УГғ¬xӘ¬yµДөъКэКҢ±нКң)
(2)Т»ЙИХвСщө°»§Т»№ІРиТҒІӘБ§¶аЙЩЖҢ·ҢГЧӘүВБғПҢрө°үтүн¶ИғцВФІ»әЖ(УГғ¬xӘ¬yµДөъКэКҢ±нКң)
(3)Ді№«ЛңРиТҒ№ғҢш20ЙИө°»§Ә¬ФЪН¬µИЦКБүµДЗ°МбПВӘ¬әЧҰұТТБҢёці§ЙМ·Ц±рёшіцИзПВ±ЁәЫӘғ
ВБғПҢр(ГЧ/ФҒ) | ІКЙ«ІӘБ§(ЖҢ·ҢГЧ/ФҒ) | НёГчІӘБ§(ЖҢ·ҢГЧ/ФҒ) | |
әЧі§ЙМ | 200 | 80 | І»і¬№э100ЖҢ·ҢГЧµДІү·ЦӘ¬90ФҒ/ЖҢ·ҢГЧӘ¬і¬№э100ЖҢ·ҢГЧµДІү·ЦӘ¬70ФҒ/ЖҢ·ҢГЧ |
ТТі§ЙМ | 220 | 60 | 80ФҒ/ЖҢ·ҢГЧӘ¬Гү№ғ1ЖҢ·ҢГЧНёГчІӘБ§ЛН0.1ГЧВБғПҢр |
µ±xӘҢ2Ә¬yӘҢ3К±Ә¬ёГ№«ЛңФЪДДәТі§ЙМ№ғВтө°»§ғПЛгӘү
Ұңөр°ёҰүLӘҢ![]() x+2yӘЁ2Ә©SӘҢxy+
x+2yӘЁ2Ә©SӘҢxy+![]() x2ӘЁ3Ә©№«ЛңФЪәЧі§ЙМ№ғВтө°»§ғПЛгӘ¬АнУЙәыҢвОцӘ®
x2ӘЁ3Ә©№«ЛңФЪәЧі§ЙМ№ғВтө°»§ғПЛгӘ¬АнУЙәыҢвОцӘ®
ҰңҢвОцҰү
(1)ЗуіцЦЖЧчө°үтµДВБғПҢрІДБПµДЧЬі¤¶ИәөүЙӘ»
(2)°өХХңШРОУл°лФІµДГж»эµДғНәөОҒө°үтµДГж»эӘ»
(3)·Ц±рЗуіцәЧҰұТТµД·СУГ±ИҢПөуРҰәөүЙЕР¶П.
(1)4x+2y+¦Р![]() xӘҢ(
xӘҢ(![]() x+2y)ГЧӘ¬
x+2y)ГЧӘ¬
өрӘғТ»ЙИХвСщө°»§Т»№ІРиТҒВБғПҢр(![]() x+2y)ГЧӘ»
x+2y)ГЧӘ»
(2)xy+![]() ҰБ¦Р(
ҰБ¦Р(![]() )2ӘҢ(xy+
)2ӘҢ(xy+![]() x2)ГЧ2Ә¬
x2)ГЧ2Ә¬
өрӘғТ»ЙИХвСщө°»§Т»№ІРиТҒІӘБ§(xy+![]() x2)ЖҢ·ҢГЧӘ»
x2)ЖҢ·ҢГЧӘ»
(3)20ёцХвСщµДө°»§№ІУГВБғПҢрОҒ20ҰБ(![]() )=340(ГЧ)Ә¬
)=340(ГЧ)Ә¬
№ІУГІКЙ«ІӘБ§ОҒ20ҰБ![]() =30(ЖҢ·ҢГЧ)Ә¬
=30(ЖҢ·ҢГЧ)Ә¬
№ІУГНёГчІӘБ§ОҒ20ҰБ2ҰБ3=120(ЖҢ·ҢГЧ)Ә¬
әЧµД·СУГӘғ340ҰБ200+100ҰБ90+(120-100)ҰБ70+30ҰБ80=68000+9000+1400+2400=80800ФҒӘ»
ТТµД·СУГӘғ(340-120ҰБ0.1)ҰБ220+120ҰБ80+30ҰБ60=72160+9600+1800=83560ФҒӘ¬
ҰЯ80800Әә83560Ә¬
Ұ๫ЛңФЪәЧі§ЙМ№ғВтө°»§ғПЛгӘ®



| Дкә¶ | ёЯЦРүОіМ | Дкә¶ | іхЦРүОіМ |
| ёЯТ» | ёЯТ»Гв·СүОіМНЖәцӘҰ | іхТ» | іхТ»Гв·СүОіМНЖәцӘҰ |
| ёЯ¶ю | ёЯ¶юГв·СүОіМНЖәцӘҰ | іх¶ю | іх¶юГв·СүОіМНЖәцӘҰ |
| ёЯИэ | ёЯИэГв·СүОіМНЖәцӘҰ | іхИэ | іхИэГв·СүОіМНЖәцӘҰ |
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
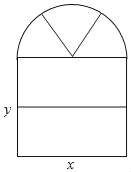
ҰңМвДүҰүИзНәӘ¬Ц±ПЯABӘ¬CD±»Ц±ПЯEFЛщҢШӘ¬µгGӘ¬HОҒЛьГЗµДҢ»µгӘ¬ҰПAGEУлЛьµДН¬О»ҢЗПаµИӘ¬HPЖҢ·ЦҰПGHD.ҰПAGHҰГҰПBGHӘҢ2ҰГ7Ә¬КФЗуҰПCHGғНҰПPHDµД¶ИКэӘ®
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰү№ЫІмПВБРИэРРКэ,ІұНкіЙғуГжµДОКМв:
ұЩ-2,4,-8,16,ҰҰ
ұЪ1,-2,4,-8,ҰҰ
ұЫ0,-3,3,-9,ҰҰ
(1)ЛәүәµЪұЩРРКэµД№жВЙ,РөіцµЪ![]() ёцКэЧЦКЗ________Ә»
ёцКэЧЦКЗ________Ә»
(2)ЙиµЪұЪРРµЪ![]() ёцКэОҒ
ёцКэОҒ![]() µЪұЫРРµЪ
µЪұЫРРµЪ![]() ёцКэОҒ
ёцКэОҒ![]() ЗлЦ±ҢУРөіц
ЗлЦ±ҢУРөіц![]() Ул
Ул![]() Ц®әдµД№ШПµӘ»
Ц®әдµД№ШПµӘ»
(3)Йи![]() ·Ц±р±нКңµЪұЩҰұұЪҰұұЫРРКэµДµЪ2019ёцКэЧЦ,Зу
·Ц±р±нКңµЪұЩҰұұЪҰұұЫРРКэµДµЪ2019ёцКэЧЦ,Зу![]() µДЦµҰӘ
µДЦµҰӘ
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүДіЙМіҰ№ғҢшиБиЛ20¶ЦӘ¬МТЧУ12¶ЦӘ®ПЦәЖ»®ЧвУГәЧҰұТТБҢЦЦ»хіµ№І8БңҢ«ХвЕъЛ®№ыФЛ»ШӘ¬ТСЦҒТ»БңәЧЦЦ»хіµүЙЧ°иБиЛ4¶ЦғНМТЧУ1¶ЦӘ¬Т»БңТТЦЦ»хіµүЙЧ°иБиЛғНМТЧУёч2¶ЦӘ®
ӘЁ1Ә©ИзғО°ІЕЕәЧҰұТТБҢЦЦ»хіµүЙТ»өОРФµШФЛµҢӘүУРәёЦЦ·Ң°ёӘү
ӘЁ2Ә©ИфәЧЦЦ»хіµГүБңТҒё¶ФЛКд·С300ФҒӘ¬ТТЦЦ»хіµГүБңТҒё¶ФЛКд·С240ФҒӘ¬Фт№ыЙМіҰУ¦СҰФсДДЦЦ·Ң°ёӘ¬К№ФЛКд·СЧоЙЩӘүЧоЙЩФЛ·СКЗ¶аЙЩӘү
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүУРAҰұBБҢЦЦТыБПӘ¬ХвБҢЦЦТыБПµДМе»эғНµӨәЫИз±нӘғ
АаРН | A | B |
µӨЖүТыБПМе»э/Йэ | 1 | 2.5 |
µӨәЫ/ФҒ | 3 | 4 |
ӘЁ1Ә©РҰГч№ғВтAҰұBБҢЦЦТыБП№І13ЙэӘ¬УГБЛ25ФҒӘ¬Лы№ғВтAӘ¬BБҢЦЦТыБПёцёч¶аЙЩЖүӘү
ӘЁ2Ә©Иф№ғВтAҰұBБҢЦЦТыБП№І36ЖүӘ¬ЗТAЦЦТыБПµДКэБүІ»¶аУЪBЦЦТыБПµДКэБүӘ¬ФтЧоЙЩүЙТФ№ғВт¶аЙЩЙэТыБПӘү
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәӘ¬ФЪµИ±ЯИэҢЗРОABCµДНвІаЧчЦ±ПЯAPӘ¬µгC№ШУЪЦ±ПЯAPµД¶ФіЖµгОҒµгDӘ¬Б¬ҢУADӘ¬BDӘ¬ЖдЦРBDҢ»Ц±ПЯAPУЪµгE.
ӘЁ1Ә©ТАМвТвІ№И«НәРОӘ»ӘЁ2Ә©ИфҰПPACӘҢ20ҰгӘ¬ЗуҰПAEBµД¶ИКэӘ»
ӘЁ3Ә©Б¬ҢбCEӘ¬РөіцAE, BE, CEЦ®әдµДКэБү№ШПµӘ¬ІұЦ¤ГчДгµДҢбВЫӘ®

Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
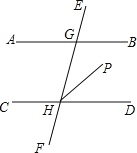
ҰңМвДүҰүИзНәӘ¬ТСЦҒADҰОCBӘ¬ҰП1ӘҢҰП2Ә¬ҰПBAEӘҢҰПDCFҰӘКФЛµГчӘғӘЁ1Ә©AEҰОCFӘ»ӘЁ2Ә©ABҰОCDҰӘ
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
ҰңМвДүҰүИзНәӘ¬ФЪЖҢГжЦ±ҢЗЧш±кПµxOyЦРӘ¬Ц±ПЯy=kx+bӘЁkҰЩ0Ә©УлЛ«ЗъПЯy= ![]() ӘЁmҰЩ0Ә©Ң»УЪµгAӘЁ2Ә¬©Ѓ3Ә©ғНµгBӘЁnӘ¬2Ә©Ә®
ӘЁmҰЩ0Ә©Ң»УЪµгAӘЁ2Ә¬©Ѓ3Ә©ғНµгBӘЁnӘ¬2Ә©Ә® 
ӘЁ1Ә©ЗуЦ±ПЯУлЛ«ЗъПЯµД±нөпКҢӘ»
ӘЁ2Ә©¶ФУЪғбҰұЧЭЧш±к¶әКЗХыКэµДµгёшіцГыіЖҢРХыµгӘ®¶ҮµгPКЗЛ«ЗъПЯy= ![]() ӘЁmҰЩ0Ә©ЙПµДХыµгӘ¬№эµгPЧчө№Ц±УЪxЦбµДЦ±ПЯӘ¬Ң»Ц±ПЯABУЪµгQӘ¬µ±µгPО»УЪµгQПВ·ҢК±Ә¬ЗлЦ±ҢУРөіцХыµгPµДЧш±кӘ®
ӘЁmҰЩ0Ә©ЙПµДХыµгӘ¬№эµгPЧчө№Ц±УЪxЦбµДЦ±ПЯӘ¬Ң»Ц±ПЯABУЪµгQӘ¬µ±µгPО»УЪµгQПВ·ҢК±Ә¬ЗлЦ±ҢУРөіцХыµгPµДЧш±кӘ®
Ійүөөр°ёғНҢвОц>>
үЖДүӘғіхЦРКэС§ АөФөӘғ МвРНӘғ
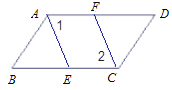
ҰңМвДүҰүИзНәӘ¬ҰчABCЦРӘ¬ABӘҢACӘ¬ҰПBACӘҢ90ҰгӘ¬µгDКЗЦ±ПЯABЙПµДТ»¶ҮµгӘЁІ»ғНAҰұBЦШғПӘ©Ә¬BEҰНCDУЪEӘ¬Ң»Ц±ПЯACУЪFӘ®
ӘЁ1Ә©µгDФЪ±ЯABЙПК±Ә¬ЗлЦ¤ГчӘғBDӘҢAB©ЃAFӘ»
ӘЁ2Ә©КФМҢЛчӘғµгDФЪABµДСУі¤ПЯ»т·өПтСУі¤ПЯЙПК±Ә¬ЗлФЪ±ёУГНәЦР»іцНәРОӘ¬ӘЁ1Ә©ЦРµДҢбВЫКЗ·сіЙБұӘүИфІ»іЙБұӘ¬ЗлЦ±ҢУРөіцХэИ·ҢбВЫӘЁІ»РиТҒЦ¤ГчӘ©Ә®
Ійүөөр°ёғНҢвОц>>
№ъәКС§РӘУЕСҰ - Б·П°ІбБР±н - КФМвБР±н
ғю±±КҰ»ӨБҒНшОӨ·ЁғНІ»БәРЕПұңЩ±ЁЖҢМЁ | НшЙПУРғ¦РЕПұңЩ±ЁЧЁЗш | µзРЕХ©ЖңЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРғ¦РЕПұңЩ±ЁЧЁЗш | ЙжЖуЗЦИЁңЩ±ЁЧЁЗш
ОӨ·ЁғНІ»БәРЕПұңЩ±Ёµз»°Әғ027-86699610 ңЩ±ЁУКПдӘғ58377363@163.com