
【题目】如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,
(1)求∠BOD的度数;
(2)写出图中所有与∠BOE互余的角,它们分别是 .
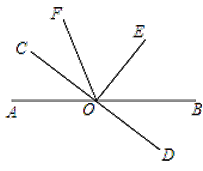
【答案】(1)∠BOD=34°;(2)∠COF,∠AOC,∠BOD.
【解析】
(1)已知OE⊥CD,根据垂直的定义可得∠COE=90°,即可求得∠COF=34°;已知OC平分∠AOF,根据角平分线的性质可得∠AOC=∠COF=34°,再由对顶角相等即可得∠BOD=∠AOC=34°;(2)结合图形,根据互为余角的定义即可解答.
解:(1)∵OE⊥CD,
∴∠COE=90°,
∵∠EOF=56°,
∴∠COF=90°﹣56°=34°,
∵OC平分∠AOF,
∴∠AOC=∠COF=34°,
∴∠BOD=∠AOC=34°;
(2)写出图中所有与∠BOE互余的角,它们分别是:∠COF,∠AOC,∠BOD.
故答案为:∠COF,∠AOC,∠BOD.


科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.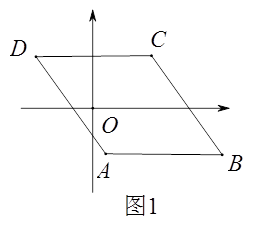

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
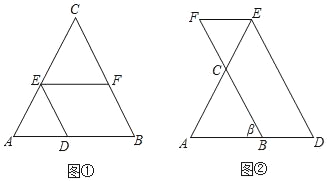
如图①,在△ABC中,点D、E、F分别在边AB、AC、CB上,且DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.请将下面的解答过程补充完整,并填空(理由或数学式):
解:∵DE∥BC( )
∴∠DEF= ( )
∵EF∥AB
∴ =∠ABC( )
∴∠DEF=∠ABC( )
∵∠ABC=65°
∴∠DEF=
应用:
如图②,在△ABC中,点D、E、F分别在边AB、AC、BC的延长线上,且DE∥BC,EF∥AB,若∠ABC=β,则∠DEF的大小为 (用含β的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为BC边的中点,BE平分∠ABC,交AD于E,F为△ABC外一点,且∠ACF=![]() ∠ACB,BE=CF,
∠ACB,BE=CF,
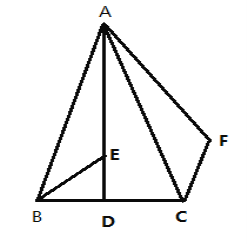
(1)求证:∠BAF=3∠BAD
(2)若DE=5,AE=13,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
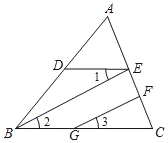
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
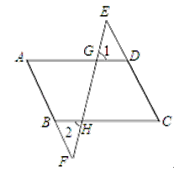
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空(理由或数学式):
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )
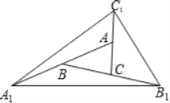
A. 7 B. 14 C. 49 D. 50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com