
【题目】如图,点A,B在反比例函数y= ![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 . 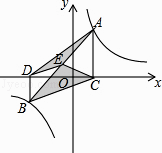
【答案】![]()
【解析】解:过点B作直线AC的垂线交直线AC于点F,如图所示. 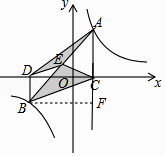
∵△BCE的面积是△ADE的面积的2倍,E是AB的中点,
∴S△ABC=2S△BCE , S△ABD=2S△ADE ,
∴S△ABC=2S△ABD , 且△ABC和△ABD的高均为BF,
∴AC=2BD,
∴OD=2OC.
∵CD=k,
∴点A的坐标为( ![]() ,3),点B的坐标为(﹣
,3),点B的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴AC=3,BD= ![]() ,
,
∴AB=2AC=6,AF=AC+BD= ![]() ,
,
∴CD=k= ![]() =
= ![]() =
= ![]() .
.
故答案为: ![]() .
.
过点B作直线AC的垂线交直线AC于点F,由△BCE的面积是△ADE的面积的2倍以及E是AB的中点即可得出S△ABC=2S△ABD , 结合CD=k即可得出点A、B的坐标,再根据AB=2AC、AF=AC+BD即可求出AB、AF的长度,根据勾股定理即可算出k的值,此题得解.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=4 ![]() ,则△CEF的面积是( )
,则△CEF的面积是( ) 
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( ) 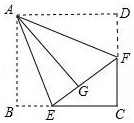
A.1.5
B.2.5
C.2.25
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.试说明:AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
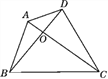
解:在△OAB中有OA+OB>AB,
在△OAD中有______________,
在△ODC中有______________,
在△________中有______________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+AD+CD+BC,
即________________________.
∴AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
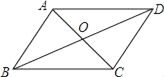
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
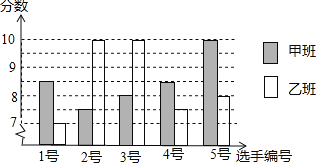
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.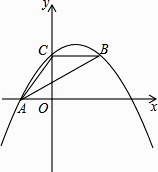
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:如果点P是锐角![]() 内一动点,如何确定一个位置,使点P到
内一动点,如何确定一个位置,使点P到![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小?
的值为最小?
![]() 问题的转化:把
问题的转化:把![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() ;
;
![]() 问题的解决:当点P到锐角
问题的解决:当点P到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 和
和![]() 的度数;
的度数;
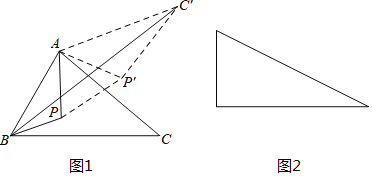
![]() 问题的延伸:如图2是有一个锐角为
问题的延伸:如图2是有一个锐角为![]() 的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com