
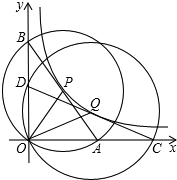
 如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B;Q是图象上异于点P的另一点,以Q为圆心、QO为半径画圆与坐标轴分别交于点C、D,则线段OA、OB、OC、OD之间的数量关系为OA•OB=OC•OD.
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B;Q是图象上异于点P的另一点,以Q为圆心、QO为半径画圆与坐标轴分别交于点C、D,则线段OA、OB、OC、OD之间的数量关系为OA•OB=OC•OD. 分析 首先过点P作PM⊥x轴于点M,PN⊥y轴于点N,设点P坐标为(m,n)(m>0,n>0),由P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,可得mn=12,又由垂径定理可得OA=2OM=2m,OB=2ON=2n,则可求得S△AOB=$\frac{1}{2}$OA•OB=24,同理可得:S△COD=$\frac{1}{2}$OC•OD=24,即可证得OA•OB=OC•OD.
解答 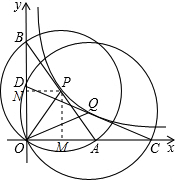 解:过点P作PM⊥x轴于点M,PN⊥y轴于点N,设点P坐标为(m,n)(m>0,n>0),
解:过点P作PM⊥x轴于点M,PN⊥y轴于点N,设点P坐标为(m,n)(m>0,n>0),
则OM=m,ON=n,
∵点P是反比例函数y=$\frac{12}{x}$(x>0)图象上一点,
∴mn=12.
由垂径定理可知,点M为OA中点,点N为OB中点,
∴OA=2OM=2m,OB=2ON=2n,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×2n×2m=2mn=2×12=24,
同理可得:S△COD=$\frac{1}{2}$OC•OD=24,
∴S△COD=S△AOB=24,
即$\frac{1}{2}$OA•OB=$\frac{1}{2}$OC•OD,
∴OA•OB=OC•OD.
故答案为:OA•OB=OC•OD.
点评 此题属于反比例函数的综合题,考查了反比例函数的图象与性质、圆周角定理、垂径定理等知识.此题的核心是考查反比例函数系数的几何意义,对本题而言,若反比例函数系数为k,则可以证明⊙P在坐标轴上所截的两条线段的乘积等于4k;对于另外一点Q所形成的⊙Q,此结论依然成立.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a,小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a,小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )| A. | 勾股定理 | B. | 勾股定理是逆定理 | ||
| C. | 直径所对的圆周角是直角 | D. | 90°的圆周角所对的弦是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-5)2+3 | B. | y=(x+5)2-3 | C. | y=(x-5)2-3 | D. | y=(x+5)2+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com