
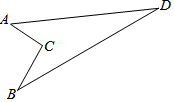
 如图,有一块耕地ACBD,已知AD=24m,BD=26m,AC⊥BC,且AC=6m,BC=8m.求这块耕地的面积.
如图,有一块耕地ACBD,已知AD=24m,BD=26m,AC⊥BC,且AC=6m,BC=8m.求这块耕地的面积. 分析 连接AB,先根据勾股定理求出AB的长,再由勾股定理的逆定理,判断出△ABD的形状,根据S四边形ADBC=S△ABD-S△ABC即可得出结论.
解答 解:连接AB,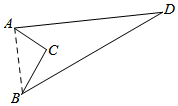
∵AC⊥BC,AC=6m,BC=8m,
∴Rt△ABC中,AB=$\sqrt{{6}^{2}+{8}^{2}}$=10m,
∵AD=24m,BD=26m,
∴AD2=242=576,BD2=262=676,AB2=1002=100,
∴AB2+AD2=BD2,
∴△ABD是直角三角形,
∴S四边形ADBC=S△ABD-S△ABC=$\frac{1}{2}$AB•AD-$\frac{1}{2}$AC•BC=$\frac{1}{2}$×10×24-$\frac{1}{2}$×8×6=120-24=96m2.
答:这块土地的面积是96m2.
点评 本题考查的是勾股定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{11}$ | B. | $\frac{9}{11}$ | C. | $\frac{5}{9}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+2<b+2 | B. | a-2>b-2 | C. | -3a<-3b | D. | -$\frac{a}{2}$<-$\frac{b}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com