
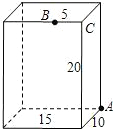
 如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )| A. | 20 | B. | 25 | C. | 30 | D. | 32 |
分析 要求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.
解答 解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图: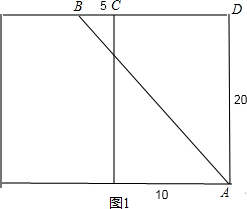
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴BD=CD+BC=10+5=15,AD=20,
在直角三角形ABD中,根据勾股定理得:
∴AB=$\sqrt{B{D}^{2}+A{D}^{2}}=\sqrt{1{5}^{2}+2{0}^{2}}$=25;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴BD=CD+BC=20+5=25,AD=10,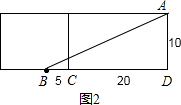
在直角三角形ABD中,根据勾股定理得:
∴AB=$\sqrt{B{D}^{2}+A{D}^{2}}=\sqrt{1{0}^{2}+2{5}^{2}}=5\sqrt{29}$;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10,高为20,点B离点C的距离是5,
∴AC=CD+AD=20+10=30,
在直角三角形ABC中,根据勾股定理得:
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{3{0}^{2}+{5}^{2}}=5\sqrt{37}$;
∵25<5$\sqrt{29}$$<5\sqrt{37}$,
∴蚂蚁爬行的最短距离是25,
故选B
点评 本题主要考查两点之间线段最短,关键是将长方体侧面展开,然后利用两点之间线段最短解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 经过我区的济南市第一条地铁R1线正紧锣密鼓施工,施工单位为了提醒司机注意绕行,在某路口设立了交通路况指示牌(如图),已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况指示牌BC的高度(可保留根号).
经过我区的济南市第一条地铁R1线正紧锣密鼓施工,施工单位为了提醒司机注意绕行,在某路口设立了交通路况指示牌(如图),已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况指示牌BC的高度(可保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1题 | B. | 2题 | C. | 3题 | D. | 4题 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,AC=8,点D在AB边上,且AD=BD=CD=5,在△ABC外,作等边△ACE.
已知:如图,△ABC中,AC=8,点D在AB边上,且AD=BD=CD=5,在△ABC外,作等边△ACE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com