
分析 (1)利用完全平方公式把(m+n$\sqrt{3}$)2展开即可得到a、b的值;
(2)利用(1)中结论得到a=m2+3n2,2mn=4,即mn=2,利用有理数的整除性确定m和n的值,然后计算a的值.
解答 解:(1)(m+n$\sqrt{3}$)2=m2+3n2+2mn$\sqrt{3}$,
所以a=m2+3n2,b=2mn;
故答案为m2+3n2,2mn;
(2)由(1)得a=m2+3n2,2mn=4,
而a、b、m、n均为正整数,
所以m=2,n=1或m=1,n=2.
所以当m=2,n=1时,a=22+3×12=7.
当m=1,n=2时,a=12+3×22=13.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.也考查了阅读理解能力.


科目:初中数学 来源: 题型:解答题
 如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).
如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
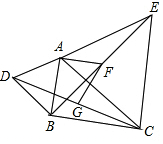 如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG.
如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
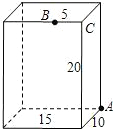 如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )| A. | 20 | B. | 25 | C. | 30 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com