
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:填空题
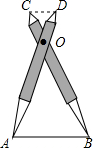 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com