Question

【题目】已知如图一，在△ABC中，AD是角平分线，AE是高，∠ABC＝30°，∠ACB＝70°．

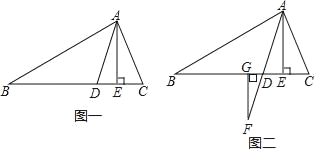
(1)求∠DAE的度数．

(2)如图二，若点F为AD延长线上一点，过点F作FG⊥BC于点G，求∠AFG的度数．

Answer 1

【答案】(1)∠DAE＝20°；(2)∠AFG＝20°．

【解析】

（1）先利用三角形内角和定理求出∠BAC＝80°，再利用角平分线求出∠BAD＝40°，进而求出∠ADC＝∠BAD+∠ABD＝70°，最后用三角形的内角和定理 即可得出结论；

（2）先判断出FG∥AE，即可得出结论．

(1)在△ABC中，

∵∠ABC＝30°，∠ACB＝70°，

∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣30°﹣70°＝80°

∵AD平分∠BAC

∴∠BAD＝∠CAD＝∠BAC＝×80°＝40°，

在△ABD中，

∠ADC＝∠BAD+∠ABD＝40°+30°＝70°

∵AE为三角形的高，

∴∠AED＝90°．

在△AED中，

∠DAE＝180°﹣∠ADE﹣∠AED＝180°﹣70°﹣90°＝20°．

(2)∵FG⊥BC∴∠FGD＝90°

∵∠AED＝90°

∴∠FGD＝∠AED

∴FG∥AE

∴∠AFG＝∠DAE

由(1)可知∠DAE＝20°

∴∠AFG＝20°．