
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 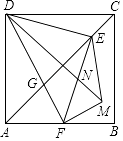
【答案】![]()
【解析】解:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE, 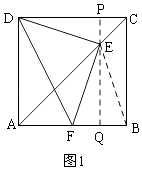
∵DC∥AB,
∴PQ⊥AB,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△PEC是等腰直角三角形,
∴PE=PC,
设PC=x,则PE=x,PD=4﹣x,EQ=4﹣x,
∴PD=EQ,
∵∠DPE=∠EQF=90°,∠PED=∠EFQ,
∴△DPE≌△EQF,
∴DE=EF,
易证明△DEC≌△BEC,
∴DE=BE,
∴EF=BE,
∵EQ⊥FB,
∴FQ=BQ= ![]() BF,
BF,
∵AB=4,F是AB的中点,
∴BF=2,
∴FQ=BQ=PE=1,
∴CE= ![]() ,
,
Rt△DAF中,DF= ![]() =2
=2 ![]() ,
,
∵DE=EF,DE⊥EF,
∴△DEF是等腰直角三角形,
∴DE=EF= ![]() =
= ![]() ,
,
∴PD= ![]() =3,
=3,
如图2,∵DC∥AB,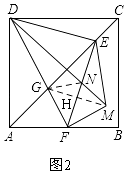
∴△DGC∽△FGA,
∴ ![]() =
= ![]() =2,
=2,
∴CG=2AG,DG=2FG,
∴FG= ![]() ×
× ![]() =
= ![]() ,
,
∵AC= ![]() =4
=4 ![]() ,
,
∴CG= ![]() ×
× ![]() =
= ![]() ,
,
∴EG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
连接GM、GN,交EF于H,
∵∠GFE=45°,
∴△GHF是等腰直角三角形,
∴GH=FH= ![]() =
= ![]() ,
,
∴EH=EF﹣FH= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
由折叠得:GM⊥EF,MH=GH= ![]() ,
,
∴∠EHM=∠DEF=90°,
∴DE∥HM,
∴△DEN∽△MNH,
∴ ![]() ,
,
∴ ![]() =
= ![]() =3,
=3,
∴EN=3NH,
∵EN+NH═EH= ![]() ,
,
∴EN= ![]() ,
,
∴NH=EH﹣EN= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
Rt△GNH中,GN= ![]() =
= ![]() =
= ![]() ,
,
由折叠得:MN=GN,EM=EG,
∴△EMN的周长=EN+MN+EM= ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
故答案为: ![]() .
.
如图1,作辅助线,构建全等三角形,根据全等三角形对应边相等证明FQ=BQ=PE=1,△DEF是等腰直角三角形,利用勾理计算DE=EF= ![]() ,PD=
,PD= ![]() =3,如图2,由平行相似证明△DGC∽△FGA,列比例式可得FG和CG的长,从而得EG的长,根据△GHF是等腰直角三角形,得GH和FH的长,利用DE∥GM证明△DEN∽△MNH,则
=3,如图2,由平行相似证明△DGC∽△FGA,列比例式可得FG和CG的长,从而得EG的长,根据△GHF是等腰直角三角形,得GH和FH的长,利用DE∥GM证明△DEN∽△MNH,则 ![]() ,得EN=
,得EN= ![]() ,从而计算出△EMN各边的长,相加可得周长.
,从而计算出△EMN各边的长,相加可得周长.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E. 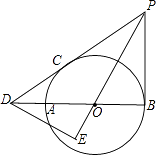
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( ) 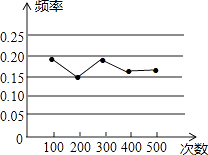
A.同时抛掷两枚硬币,落地后两枚硬币正面都朝上
B.一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C.抛一个质地均匀的正方体骰子,朝上的面点数是3
D.一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店因换季将某种服装打折销售,每件服装如果按标价的4折出售将亏40元,而按标价8折出售将赚40元.问:
(1)每件服装的标价是多少元?
(2)每件服装的成本是多少元?
(3)为了保证不亏损,最多可以打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )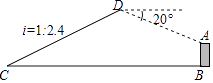
A.29.1米
B.31.9米
C.45.9米
D.95.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )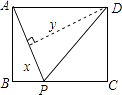
A.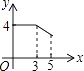
B.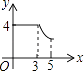
C.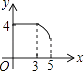
D.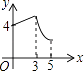
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com