问题提出：从A到B共有8个台阶，如果某同学在上台阶时，可以一步1个台阶，也可以一步2个台阶．那么该同学从A走到B共有多少种不同的走法？
问题探究：为解决上述实际问题，我们先建立如下数学模型：
用若干个边长都为1的正方形（记为1×1矩形）和若干个边长分别为1和2的矩形（记为1×2矩形），如图1，要拼成一个边长分别为1和n的矩形（记为1×n矩形），如图2，有多少种不同的拼法？（设A
1×n表示不同拼法的个数）
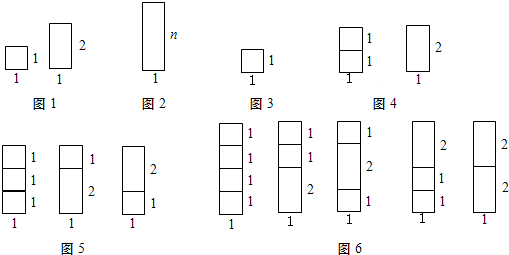
为解决上述数学模型问题，我们采取的策略和方法是：一般问题特殊化．
探究一：先从最特殊的情形入手，即要拼成一个1×1矩形，有多少种不同拼法？
显然，只有1种拼法，如图3，即A
1×1=1种．
探究二：要拼成一个1×2矩形，有多少种不同拼法？不难看出，有2种拼法，如图4，即A
1×2=2种．
探究三：要拼成一个1×3矩形，有多少种不同拼法？拼图方法可分为两类：一类是在图4这2种1×2矩形
上方，各拼上一个1×1矩形，即这类拼法共有A
1×2=2种；另一类是在图3这1种1×1矩形上方拼上一个1×2矩形，即这类拼法有A
1×1=1种，如图5．即A
1×3=A
1×2+A
1×1=2+1=3（种）．
探究四：要拼成一个1×4矩形，有多少种不同拼法？拼图方法可分为两类：一类是在图5这3种1×3矩形上方，各拼上一个1×1矩形，即这类拼法共有A
1×3=3种；另一类是在图4这2种1×2矩形上方，各拼上一个1×2矩形，即这类拼法共有A
1×2=2种，如图6．即A
1×4=A
1×3+A
1×2=3+2=5（种）．
探究五：要拼成一个1×5矩形，有多少种不同拼法A
1×5？仿照上述探究过程进行解答，并求出A
1×5（不需画图）．
探究六：一般的，要拼成一个1×n矩形（n≥3的整数），有A
1×n=
种不同拼法．（已知A
1×（n-1）=a，A
1×（n-2）=b，）
问题解决：把“问题提出”中的实际问题，转化为“问题探究”中的数学模型，并进行解答．
如图，在直角三角形中，两直角边长为a，b斜边上的高为h，判断以ab，ah，bh为边长的三角形形状并说明理由．
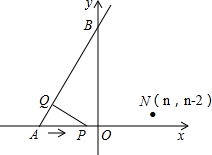如图，已知射线AB与x轴和y轴分别交于点A（-3，0）和点B（0，3
如图，在平行四边形ABCD中，M是CD的中点，AB=2BC，BM=a，AM=b，则CD的长为（ ）