
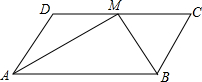
 如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )A、
| ||
B、a+
| ||
C、
| ||
D、
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| MA2+MB2 |
| a2+b2 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
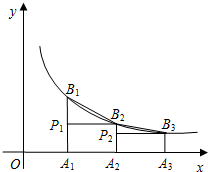 如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
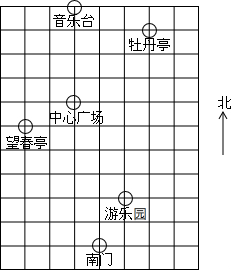 春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)
春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)查看答案和解析>>
科目:初中数学 来源: 题型:
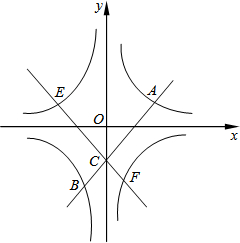 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=| 1 |
| x |
| -1 |
| x |
| 1 |
| x |
| -1 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com