
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
这些数据说明:植物每天高度增长量 ![]() 关于温度
关于温度 ![]() 的函数是反比例函数、一次函数和二次函数中的一种.
的函数是反比例函数、一次函数和二次函数中的一种.
(1)你认为是哪一种函数,并求出它的函数关系式;
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?请直接写出结果.
【答案】
(1)解:选择二次函数,设 ![]() ,
,
得  ,解得
,解得 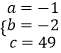
∴y关于x的函数关系式是 ![]() .
.
不选另外两个函数的理由:注意到点(0,49)不可能在任何反比例函数图象上,所以y不是x的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y不是x的一次函数
(2)解:由(1),得 ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴当x=-1时,y有最大值为50.
即当温度为-1℃时,这种植物每天高度增长量最大
(3)解: ![]()
【解析】(1)根据表格得到点(0,49)不可能在任何反比例函数图象上,所以y不是x的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y不是x的一次函数;得到是二次函数,把三个点的坐标代入,求出y关于x的二次函数关系式;(2)由(1)的函数关系式,得到顶点式,求出这种植物每天高度增长量的最大值;(3)根据表格和已知在10天内要使该植物高度增长量的总和超过250mm,得到x的取值范围.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】二次函数 ![]() 的部分图像如图所示,图像过点
的部分图像如图所示,图像过点 ![]() ,对称轴为直线
,对称轴为直线 ![]() ,下列结论:(1)
,下列结论:(1) ![]() ;(2)
;(2) ![]() ;(3)若点
;(3)若点 ![]() 、点
、点 ![]() 、点
、点 ![]() 在该函数图像上,则
在该函数图像上,则 ![]() ;(4)若方程
;(4)若方程 ![]() 的两根为
的两根为 ![]() 和
和 ![]() ,且
,且 ![]() ,则
,则 ![]() .其中正确结论的序号是.
.其中正确结论的序号是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
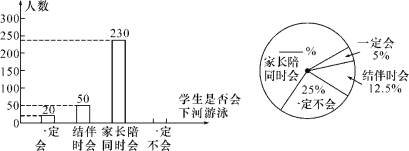
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB=DC=AD,BD=AC,BD、AC相交于点O.
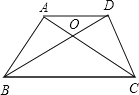
(1)求证:△ABO≌△DCO;
(2)写出图中所有与∠ACB相等的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.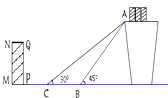
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物 ![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
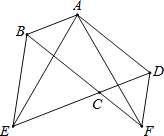
(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.若直线CE垂直于△ABC的一边,则∠BEC=____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)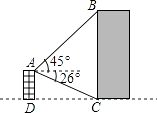
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com