Question

【题目】已知△ABC中，∠A=60°，∠ACB=40°，D为BC边延长线上一点，BM平分∠ABC，E为射线BM上一点．若直线CE垂直于△ABC的一边，则∠BEC=____°．

Answer 1

【答案】10°或50°或130°

【解析】

分三种情况讨论：①当CE⊥BC时；②当CE⊥AB时；③当CE⊥AC时；根据垂直的定义和三角形内角和计算即可得到结论．

解：①如图1，当CE⊥BC时，

∵∠A=60°，∠ACB=40°，

∴∠ABC=80°，

∵BM平分∠ABC，

∴∠CBE=∠ABC=40°，

∴∠BEC=90°-40°=50°；

②如图2，当CE⊥AB时，

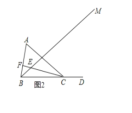
∵∠ABE=∠ABC=40°，

∴∠BEC=90°+40°=130°；

③如图3，当CE⊥AC时，

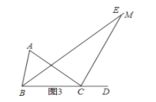
∵∠CBE=40°，∠ACB=40°，

∴∠BEC=180°-90°-40°-40°=10°；

综上所述：∠BEC的度数为10°，50°，130°，

故答案为：10°，50°，130°．