
【题目】在Rt△ABC中,斜边AB=10,直角边AC=8,以C为圆心,r为半径,若要使⊙C与边AB只有一个公共点,则r的取值范围是 .
【答案】r= ![]() 或6<r≤8
或6<r≤8
【解析】解:如图,∵斜边AB=10,直角边AC=8,∴BC= ![]() =6.
=6.
当圆和斜边相切时,则半径即是斜边上的高,r=CD= ![]() =
= ![]() ;
;
当圆和斜边相交,且只有一个交点在斜边上时,可以让圆的半径大于短直角边而小于长直角边,则6<r≤8.
所以答案是:r= ![]() 或6<r≤8.
或6<r≤8.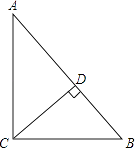
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对直线与圆的三种位置关系的理解,了解直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


科目:初中数学 来源: 题型:
【题目】下列四个选项中的表述,一定正确的是( )
A.经过半径上一点且垂直于这条半径的直线是圆的切线
B.经过半径的端点且垂直于这条半径的直线是圆的切线
C.经过半径的外端且垂直于这条半径的直线是圆的切线
D.经过一条弦的外端且垂直于这条弦的直线是圆的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
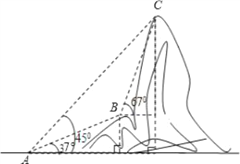
【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?
(精确到米,参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin67°≈
,sin67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图: 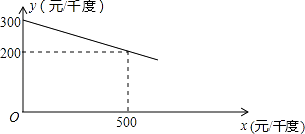
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=5m+600,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为 ![]() 的半圆后得到图形P2 , 然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3 , P4 , …,Pn , …,记纸板Pn的面积为Sn , 试通过计算S1 , S2 , 猜想得到Sn﹣1﹣Sn=(n≥2).
的半圆后得到图形P2 , 然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3 , P4 , …,Pn , …,记纸板Pn的面积为Sn , 试通过计算S1 , S2 , 猜想得到Sn﹣1﹣Sn=(n≥2). 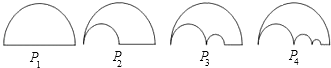
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,潜望镜中的两个镜片AB和CD是平行的,光线经过镜子反射时,∠AEN=∠BEF,∠EFD=∠CFM,那么进入潜望镜的光线NE和离开潜望镜的光线FM是平行的吗?说明理由.
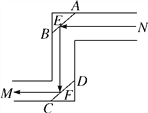
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.


端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC ,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com