
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】已知直线 y= -x+5交x轴于A,交y轴于B,直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
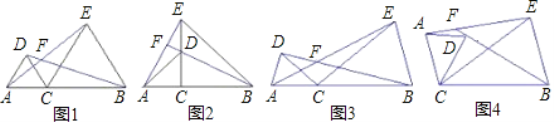
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB=______,如图2,若∠ACD=90°,则∠AFB=______,如图3,若∠ACD=α,则∠AFB=______(用含α的式子表示);
(2)设∠ACD=α,将图3中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图4,试探究∠AFB与α的数量关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
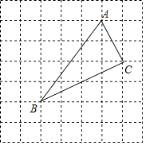
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
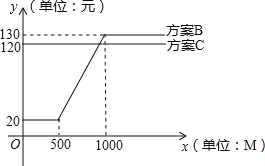
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)1-4+3-0.5
(2)(![]() )×6
)×6
(3)40×(-5)-(-3)÷![]()
(4)-14+![]() -2×(-2)2
-2×(-2)2
(5)32-(-![]() )×
)×![]() +(-8)÷
+(-8)÷![]()
(6)(-![]() )3+
)3+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC是等腰锐角三角形,AB=AC(![]() ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com