
分析 把小数化为分数、把除法化为乘法,然后根据实数运算法则进行计算.
解答 解:原式=$\frac{4}{5}$×$\frac{2}{11}$+$\frac{24}{5}$×(-$\frac{2}{7}$)-$\frac{11}{5}$×$\frac{7}{3}$+$\frac{4}{5}$×$\frac{9}{11}$
=$\frac{4}{5}$×($\frac{2}{11}$+$\frac{9}{11}$)-$\frac{48}{35}$-$\frac{77}{15}$
=$\frac{4}{5}$-$\frac{48}{35}$-$\frac{77}{15}$
=$\frac{84-144-539}{105}$
=-$\frac{599}{105}$.
点评 本题考查了有理数的乘法和除法.在进行有理数的乘法运算时,要灵活运用运算律.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一块20米,宽为8米的矩形空地,计划在其中修建两条人行通道(黑色区域),剩余绿地面积之和为126米2,若纵向的人行横道的宽是横向的人行通道的宽的2倍.
如图,有一块20米,宽为8米的矩形空地,计划在其中修建两条人行通道(黑色区域),剩余绿地面积之和为126米2,若纵向的人行横道的宽是横向的人行通道的宽的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
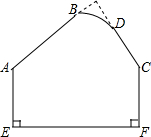 如图所示的模板,规定:AB、CD的延长线应相交成80°的角,因交点不在模板上,不便测量,工人师傅测得∠BAE=124°,∠DCF=155°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
如图所示的模板,规定:AB、CD的延长线应相交成80°的角,因交点不在模板上,不便测量,工人师傅测得∠BAE=124°,∠DCF=155°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
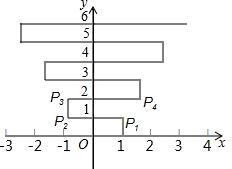 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )| A. | (100,50) | B. | (50,50) | C. | (25,50) | D. | (26,50) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com