
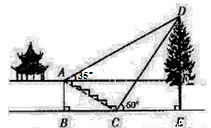
(本题10分)如图,某校综合实践活动小组的同学欲测量公园内一棵树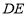 的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端
的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端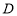 的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端
的仰角为35°,朝着这棵树的方向走到台阶下的点C处,测得树顶端 的仰角为60°.已知点A 的高度AB为
的仰角为60°.已知点A 的高度AB为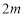 ,台阶AC的坡度为
,台阶AC的坡度为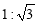 (即
(即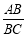 ),且
),且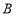 、
、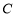 、
、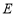 三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65°
三点在同一条直线上.请根据以上条件求出树DE的高度(参考数据:tan65°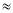 2.1,cos65°
2.1,cos65° 0.4, sin35°
0.4, sin35° 0.6,tan35°
0.6,tan35° 0.7,
0.7,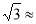 1.7,结果保留一位小数).
1.7,结果保留一位小数).
科目:初中数学 来源:2015年初中毕业升学考试(山东德州卷)数学(解析版) 题型:填空题
(2015山东省德州市,15,4分)在射击比赛中,某运动员的6次射击成绩(单位:环)为:7,8,10,8,9,6.计算这组数据的方差为 .
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:解答题
(12分)如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.
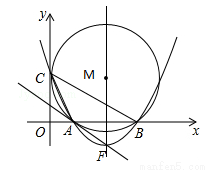
(1)则点A、B、C的坐标分别是A(__,__),B(__,__),C(__,__);
(2)设经过A、B两点的抛物线解析式为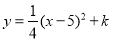 ,它的顶点为F,求证:直线FA与⊙M相切;
,它的顶点为F,求证:直线FA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级5月第二次适应测试数学试卷(解析版) 题型:填空题
如图,矩形ABCD中,AB=2BC,E是AB上一点,O是CD上一点,以OC为半径作⊙O,将△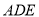 折叠至△
折叠至△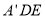 ,点
,点 在⊙O上,延长
在⊙O上,延长 交BC延长线于F,且恰好过点O,过点D作⊙O的切线交BC延长线于点G.若FG=1,则AD= ,⊙O半径= .
交BC延长线于F,且恰好过点O,过点D作⊙O的切线交BC延长线于点G.若FG=1,则AD= ,⊙O半径= .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级5月第二次适应测试数学试卷(解析版) 题型:选择题
抛物线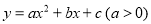 的对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),则它与x轴另一个交点的坐标为( )
的对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),则它与x轴另一个交点的坐标为( )
A.(-2,0) B.(-1,0) C.(2,0) D.(5,0)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级下学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)(1)问题情境:如图(1),已知,锐角∠AOB内有一定点P,过点P任意作一条直线MN,分别交射线OA、OB于点M、N.将直线MN绕着点P旋转,旋转过程中△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
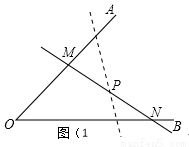
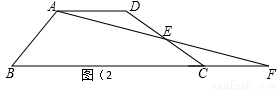
方法探究:小明与小亮二人一起研究,一会儿,小明说有办法了.小亮问:“怎么解决?”小明画出了图(2)的四边形,说:“四边形ABCD中,AD//BC,取DC边的中点E,连结AE并延长交BC的延长线于点F.显然有△ADE≌△FCE,则S四边形ABCD=S△ABF(S表示面积).借助这图和图中的结论就可以解决了.”
请你照小明提供的方法完成“问题情境”这个问题.
(2)实际应用:如图(3),若在道路OA、OB之间有一村庄Q发生疫情,防疫部门计划以公路OA、OB 和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB = 70°,∠POB = 30°,OP= 4km,试求△MON 的面积.(结果精确到0.1km2)
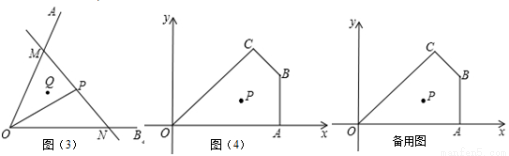
(3)拓展延伸:如图(4),在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、(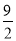 ,
, )、(4,2),过点P的直线l与四边形OABC 一组对边相交,将四边形OABC分成两个四边形,则其中以点O为顶点的四边形的面积的最大值是 .
)、(4,2),过点P的直线l与四边形OABC 一组对边相交,将四边形OABC分成两个四边形,则其中以点O为顶点的四边形的面积的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com