


|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:山东省凤城中学2011-2012学年八年级上学期期中考试数学试题 题型:044
数学课上,陈老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图,确定线段AE与DB的大小关系,请你直接写出结论:AE________DB(填“>”,“<”或“=”).

(2)一般情况,启发解答
解:题目中,AE与DB的大小关系是:AE________CB(填“>”,“<”或“=”).理由如下:如图,过点E作EF∥BC,交AC于点F.

(请你完成以下解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
数学课上,陈老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点![]() 为
为![]() 的中点时,如图1,确定线段
的中点时,如图1,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:![]()
![]() (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
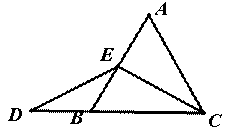

(2)一般情况, 启发解答
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(请你完成以下解答过程)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年内蒙古鄂尔多斯市大兴中学九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com